Lektion 3 - Wahrscheinlichkeitsbegriffe und Kombinatorik

3.4 Kombinatorik - Fakultät

Fakultät n!

Die Fakultät n! einer Zahl n ist das Produkt

mit  0! = 1

Die Anwendung dieser mathematischen Funktion bezieht sich in der Statistik meist auf die Anzahl der möglichen Anordnungen von n Elementen und wird üblicherweise als Anzahl von Permutationen bezeichnet.

Dazu das folgende Beispiel:

Im Regal eines Einzelhändlers sollen die 5 Warenarten A, B, C, D und E in den vorhandenen 5 Reihen untergebracht werden. Im Zusammenhang mit der Überlegung, welche Warenart in welcher Reihe die meiste Aufmerksamkeit auf sich lenkt, stellt sich die Frage, wieviele Möglichkeiten der Anordnung es überhaupt gibt.

Die Anzahl der Permutationen von 5 verschiedenen Elementen beträgt

5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 120

 

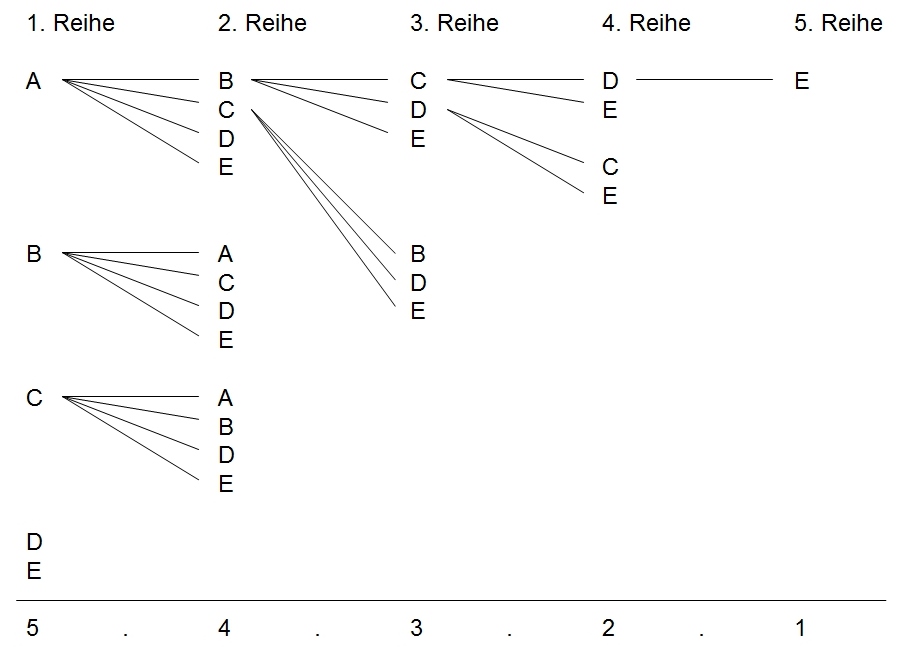
Dieses Ergebnis der Permutationen lässt sich leicht nachvollziehen, wenn wir uns die Möglichkeiten der Anordnungen für jeden Platz (Reihe im Regal) vorstellen.

Für die erste Reihe können alle 5 Warenarten ausgewählt werden, für die zweite Reihe die verbleibenden 4, für die dritte Reihe die übrigen 3 usw.