Lektion 3 - Wahrscheinlichkeitsbegriffe und Kombinatorik
3.3.1 A-priori- und A-posteriori-Wahrscheinlichkeiten
Das Ereignis, dass eine Person eine bestimmte Krankheit hat, trete mit der Wahrscheinlichkeit P(A) = 0,002 ein, d.h. 2 von 1.000 Personen haben diese Krankheit.
P(A) nennt man die A-priori-Wahrscheinlichkeit von A.
Die Wahrscheinlichkeit, dass eine Person nicht an der Krankheit A erkrankt ist, beträgt dann P(Ā) = 0,998.
In einem Test soll ermittelt werden, ob eine Person diese Krankheit hat. Das Ereignis B bedeutet dann, dass der Test positiv ausfällt - d.h. dass angezeigt wird, dass die Person die Krankheit hat.
P(B) ist die A-priori-Wahrscheinlichkeit von B.
Damit lauten die Ereignisse:
A = „krank“, Ā = „nicht krank“, B = „Test positiv“, ![]() = „Test negativ“.
= „Test negativ“.
Der pharmazeutische Anbieter des Tests garantiert, dass der Test die Krankheit mit einer Wahrscheinlichkeit von 0,99 erkennt: Damit ist P(B|A) = 0,99 und P(B|Ā) = 0,01.
Frage: Wie wahrscheinlich ist das Vorliegen einer Krankheit, wenn das Testergebnis positiv ist?
oder: Wie wahrscheinlich ist das Vorliegen keiner Erkrankung bei positivem Testergebnis = falsch positives Testergebnis?
Satz von Bayes:
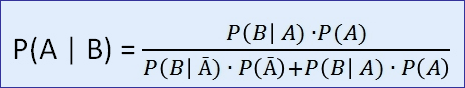
und im Beispiel:
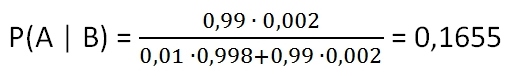
Die A-posteriori-Wahrscheinlichkeit, dass der Test „richtig positiv“ entscheidet, ist gleich 16,6%.
Damit ist die Komplementär-Wahrscheinlichkeit, dass der Test „falsch positiv“ entscheidet, erstaunlich hoch: 83,4%.
In einer Kreuztabelle (angewandt auf insgesamt 100.000 Personen) lässt sich dies wie folgt darstellen:
| Person ist... | krank | gesund | Summe | ||
| Testergebnis ist... | A | Ā | |||
| positiv | B | in % | 99,00 | 1,00 | 1,20 |
| absolut | 198 | 998 | 1.196 | ||
| negativ | in % | 1,00 | 99,00 | 99,80 | |
| absolut | 2 | 98.802 | 98.804 | ||
| Summe | in % | 0,20 | 99,80 | 100,00 | |
| absolut | 200 | 99.800 | 100.000 |
Wahrscheinlichkeit für falsch positiv (in %): 998,00 / 1.196,00 · 100 = 83,44 %
Wahrscheinlichkeit für richtig positiv (in %): 198,00 / 1.196,00 · 100 =16,56 %