Kapitel 9 - Lageparameter

9.6 Geometrisches Mittel

Bestehen die Merkmalswerte aus Wachstumsraten, Wachstumsfaktoren oder Zinsfaktoren, die über eine Folge von Perioden hinweg beobachtet werden, ist als Durchschnittswert das geometrische Mittel zu verwenden.

Das geometrische Mittel ist definiert als:

$\mathsf{ \large{ G = \sqrt[\LARGE{n}]{\strut \large {x_1\cdot x_2\cdot ... \cdot x_n} } } }$

Die gebräuchlichsten Anwendungen des geometrischen Mittels finden sich in der Berechnung der durchschnittlichen Wachstumsrate bzw. der Durchschnittsverzinsung.

Beispiel mehrjährige Verzinsung

Ein Bundesschatzbrief mit einer Laufzeit von sieben Jahren werde beginnend mit dem ersten Jahr zu folgenden Zinssätzen verzinst:

Zins r_t :

2,5 %

3,0 %

3,5 %

4,25 %

4,5 %

5,0 %

Wie hoch ist die Durchschnittsverzinsung?

Zunächst müssen die Zinssätze r_t über die Beziehungen 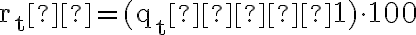$\mathrm{ r_t = (q_t – 1)\cdot100 }$ in Zinsfaktoren umgerechnet werden:

Zinsfaktor q_t :

1,025

1,03

1,035

1,0425

1,045

1,05

Dann ergibt sich für das geometrische Mittel:

$\mathsf{ \large{ G = \sqrt[\LARGE{7}]{\strut \normalsize {1,025\cdot 1,03\cdot 1,035\cdot 1,0425\cdot 1,045\cdot 1,05\cdot 1,05}} = \sqrt[\LARGE{7}]{\strut \normalsize {1,3124}} = \normalsize {1,0396} }}$

Mit dem Bundesschatzbrief erzielt der Anleger eine durchschnittliche Verzinsung von 3,96 % =

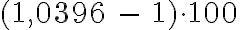$\mathsf{(1,0396 - 1)\cdot100 }$ pro Jahr.

Das geometrische Mittel hat die Eigenschaft, über n Perioden hinweg denselben Effekt zu erzielen wie die sukzessive Multiplikation der n Werte.

Hier folgt ein

Lehrvideo: Geometrisches Mittel

	Glossar