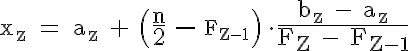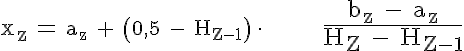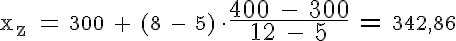Kapitel 9 - Lageparameter
9.4 Zentralwert (Median) und Quantile
(1) Zentralwert
- Urliste
Im Falle einer ungeraden Anzahl von Beobachtungswerten ist
Im Fall einer geraden Anzahl n von Beobachtungswerten genügt jeder Wert im Intervall
![\mathsf{\Large{ \left[x_{\LARGE{\frac{n}{2}}} ; x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}} \mathsf{\Large{ \left[x_{\LARGE{\frac{n}{2}}} ; x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}}](https://ilearn.th-deg.de/filter/tex/pix.php/a77acf523536c602d53ebc0fa4c55de1.png)
der obigen Definition. Man bestimmt der Einfachheit halber die Intervallmitte als Näherungswert des Zentralwerts
Beispiel: Lebensdauer von Ventilen nach der Größe geordnet
| Beobachtung i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Dauer in Std. xi | 210 | 230 | 240 | 260 | 280 | 330 | 350 | 360 | 370 | 380 | 390 | 400 | 420 | 440 | 460 | 480 |
Welche Lebensdauer wird von 50 Prozent der Ventile erreicht oder unterschritten?
Der Zentralwert liegt zwischen 360 und 370 und beträgt (gemäß der obigen Näherungsformel) 365.
→ Die Hälfte der beobachteten Ventile hat eine Lebensdauer von 365 Stunden und weniger.
- Häufigkeitsverteilung:
Im Fall einer Häufigkeitsverteilung ist der Zentralwert der Wert, bei dem die absolute kumulierte Häufigkeit den Wert n/2 bzw. die relative kumulierte Häufigkeit den Wert von 0,5 bzw. 50 Prozent erreicht oder erstmals überschreitet.
Bei einer klassierten Häufigkeitsverteilung kann der Zentralwert innerhalb der Klasse, in der der Zentralwert liegt, durch lineare Interpolation mit Hilfe der absoluten oder relativen kumulierten Häufigkeiten ermittelt werden. (Der Index Z bezeichnet die Klasse, in der der Zentralwert liegt.)
Beispiel: Lebensdauer von Ventilen
|
[aj; bj[ |
fj |
Fj |
|
200 - 300 |
5 |
5 |
|
300 - 400 |
7 |
12 |
|
400 - 500 |
4 |
16 |
|
Summe |
16 |
Welche Lebensdauer wird von 50% der Ventile erreicht oder unterschritten?
→ Der Zentralwert liegt in der Klasse 300 – 400
Innerhalb dieser Klasse wird linear interpoliert:
→ Mindestens 50 Prozent der Ventile erreicht eine Lebensdauer von 342,86 Stunden und weniger und mindestens 50 Prozent der Ventile hat eine Lebensdauer von 342,86 Stunden und mehr.
(2) Quantile
Das Prinzip für die Ermittlung des Zentralwerts lässt sich verallgemeinern, wenn man an Stelle der 50 % Grenze andere Prozentsätze verwendet. Allgemein spricht man dann von den Quantilen einer Verteilung. Die allgemeine Definition für die Quantile lautet:
Ein p % Quantil ist dadurch charakterisiert, dass mindestens p % der Beobachtungen einen Wert kleiner gleich und mindestens (1 – p) % einen Wert größer oder gleich dem Wert xp annehmen.
Insbesondere die Quartile mit 25 % bzw. 75 % werden in der Praxis häufig verwendet, ebenso die Dezile, insbesondere das unterste 10 % Dezil und das oberste 90 % Dezil.
So besagt z.B. der oberste 90% Dezilwert, dass z.B. mindestens 90 Prozent der Bevölkerung eine Körpergröße von maximal x90 cm erreicht und mindestens 10% der Bevölkerung eine Körpergröße hat, die gleich oder größer x90 cm ist.
 |
|---|
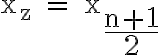
![\mathsf{\Large{x_z = \frac{1}{2} \left[x_{\LARGE {\frac{n}{2}}} + x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}} \mathsf{\Large{x_z = \frac{1}{2} \left[x_{\LARGE {\frac{n}{2}}} + x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}}](https://ilearn.th-deg.de/filter/tex/pix.php/466d489219add38dd129aff6961702f8.png)
![\mathsf{\Large{x_z = \frac{1}{2}\left[\normalsize{360+370}\right] = \normalsize{365}}} \mathsf{\Large{x_z = \frac{1}{2}\left[\normalsize{360+370}\right] = \normalsize{365}}}](https://ilearn.th-deg.de/filter/tex/pix.php/0743ec73a9c0d60800aad2155ecc7063.png)