Kapitel 9 - Lageparameter
9.5 Arithmetisches Mittel
Das arithmetische Mittel wird unter Verwendung der Urliste bzw. der Häufigkeitsverteilung wie folgt berechnet (siehe auch die entsprechenden Abschnitte in den Kapiteln 6 und 7):
Beispiel: Lebensdauer von Ventilen
| Beobachtung i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Summe |
| Dauer in Std. xi |
280 |
330 |
260 |
440 |
420 |
240 |
480 |
360 |
460 |
400 |
230 |
210 |
350 |
370 |
380 |
390 |
5600 |
Wie hoch ist die durchschnittliche Lebensdauer?
Das arithmetische Mittel beträgt 350.
Die beobachteten Ventile hatten im Durchschnitt eine Lebensdauer von 350 Stunden.
Schwerpunkteigenschaft des arithmetischen Mittels
Die Summe der Abweichungen vom arithmetischen Mittel bzw. der Durchschnitt d dieser Abweichungen ist gleich 0:
Das arithmetische Mittel liegt demnach so zentral in einer Verteilung, dass sich positive und negative Abweichungen der Merkmalswerte in der Summe ausgleichen. Deshalb werden bei der Berechnung der durchschnittlichen absoluten Abweichung die Differenzen zwischen den Merkmalswerten und dem Lageparameter absolut genommen.
Für eine Beobachtungsreihe mit den Werten 3, 6, 10, 11, 13 und 14 und dem arithmetischen Mittel von 9,5 gilt somit:
Bei klassierten Daten ist der exakte Wert von ![]() nicht zu ermitteln; man berechnet ersatzweise das gewogene arithmetische Mittel aus Klassenmitten mit den Klassenhäufigkeiten als Gewichte (siehe Lektion 7).
nicht zu ermitteln; man berechnet ersatzweise das gewogene arithmetische Mittel aus Klassenmitten mit den Klassenhäufigkeiten als Gewichte (siehe Lektion 7).
Beispiel: Lebensdauer von Ventilen
|
[aj; bj[ |
fj |
mj |
fjmj |
|
200 - 300 |
5 |
250 |
1250 |
|
300 - 400 |
7 |
350 |
2450 |
|
400 - 500 |
4 |
450 |
1800 |
|
Summe |
16 |
5500 |
Wie hoch ist die durchschnittliche Lebensdauer?
Das aus Klassenmitten errechnete arithmetische Mittel beträgt 343,75, d.h. die Ventile hatten im Durchschnitt eine Lebensdauer von etwa 343,75 Stunden.
 |
|---|
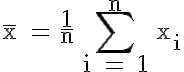
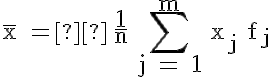
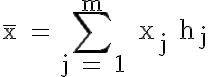
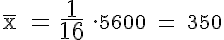
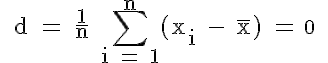
![\mathsf{ F(M) = \Large {\frac{1}{6}} \normalsize {\left[ (3 - 9,5) + (6 - 9,5) + (10 - 9,5) + (11 - 9,5) + (13 - 9,5) + (14 - 9,5)\right] = 0 }} \mathsf{ F(M) = \Large {\frac{1}{6}} \normalsize {\left[ (3 - 9,5) + (6 - 9,5) + (10 - 9,5) + (11 - 9,5) + (13 - 9,5) + (14 - 9,5)\right] = 0 }}](https://ilearn.th-deg.de/filter/tex/pix.php/09bae0756005a78c06718d7f1e78b592.png)