Kapitel 2 - Einführung in die Wahrscheinlichkeitsrechnung

2.10 Wahrscheinlichkeitsbaum

Definition und Anwendung bedingter Wahrscheinlichkeiten können graphisch mit Hilfe eines Wahrscheinlichkeitsbaumes gezeigt werden.

Hier werden insgesamt drei Wahrscheinlichkeitsverteilungen dargestellt.

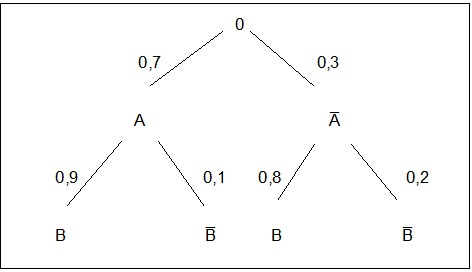
Zunächst sehen wir die Verteilung der Variablen "Geschlecht" mit den beiden Wahrscheinlichkeiten 0,7 für „männlich“ (Ereignis A) und 0,3 für „weiblich“ (Ereignis  A̅). 

Dann folgen die beiden Verteilungen der Variablen „Zufriedenheit mit dem Hotelzimmer“ mit den Wahrscheinlichkeiten 0,9 und 0,1 bei den männlichen sowie 0,8 und 0,2 bei den weiblichen  Hotelgästen. Hier liegen  bedingte Wahrscheinlichkeiten vor. Die Wahrscheinlichkeit  dafür, dass ein Gast zufrieden ist (Ereignis B), beträgt unter de r Bedingung, dass er männlich ist,  0,9 (Wahrscheinlichkeit P(B|A)) etc.

Wir können für die insgesamt vier Zweige des Wahrscheinlichkeitsbaumes die dazugehörigen Wahrscheinlichkeiten berechnen. 

Hier noch ein