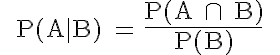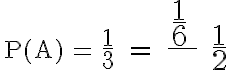Kapitel 2 - Einführung in die Wahrscheinlichkeitsrechnung

2.9 Bedingte Wahrscheinlichkeit

Eine bedingte Wahrscheinlichkeit P(A|B) gibt die Wahrscheinlichkeit für das Ereignis A an, unter der Bedingung, dass B bereits eingetreten ist oder eintritt oder eintreten wird. 

$\mathsf{ \large{ P(A|B) = \Large{\frac{P(A\ \cap \ B)}{P(B)} } }}$

Damit wird die Anzahl der möglichen Ergebnisse von B zur Bezugsgröße und wir dividieren - analog den Wahrscheinlichkeiten - die Mächtigkeit (Anzahl Elemente) der Menge A ∩ B durch die Mächtigkeit der Menge B.  

Beispiel: Würfelwurf

Wir definieren das Ereignis B „ungerade Zahlen“ und das Ereignis A  „Augenzahl 5“.

Damit ergibt sich als bedingte Wahrscheinlichkeit für A unter der Bedingung B 1/3.

Wenn wir wissen, dass Ereignis B eingetreten ist - d.h. eines der möglichen Ergebnisse (1, 3, 5) -, dann ist - unter dieser Bedingung - die Wahrscheinlichkeit für A

$\mathsf{ \large{P(A)} = \Large{\frac{1}{3} = \frac{ \LARGE{\frac{1}{6} }} {\LARGE{ \frac{1}{2} }} } }$

Und hier noch ein ergänzendes 

• Lehrvideo: Zweidimensionale und bedingte Wahrscheinlichkeit
  

	Glossar