Interaktives Buch

1. Lineare Gleichungen

Inhalt des Videos: Unterkapitel 1 

 

Dieser Abschnitt beschäftigt sich mit Gleichungen, die entweder direkt in der Form ax + b = 0 vorliegen oder durch zulässige Operationen in diese Form zu überführen sind. Hierbei handelt es sich um eine lineare Gleichung oder eine Gleichung ersten Grades, wobei  gilt. 

 

Zulässige Gleichungsoperationen oder äquivalente Umformung

Jede auf eine Gleichung angewendete Operation muss auf beide Seiten der Gleichung solange angewendet werden, bis die Variable auf einer Seite isoliert ist.

Äquivalente Gleichungen erhält man, wenn zu bzw. von beiden Seiten der selbe Wert addiert bzw. subtrahiert, eine Gleichung mit demselben Wert ≠ 0 multipliziert bzw. dividiert wird. Hierbei wird von äquivalenter Umformung gesprochen.

  

   

                                                                  

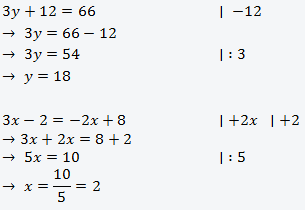
Die Gleichung ax + b = 0  ist eindeutig lösbar, wobei die Gleichung entweder eine oder mehrere Lösungen haben kann.

  

     

  

Des Weiteren kann  die Gleichung für ihre variablen Werte gültig oder widersprüchlich sein.

Die Lösungsversuche einer widersprüchlichen Gleichung scheitern daran, dass sich zwar ebenfalls die Variablen gegenseitig aufheben, die eine Seite der Gleichung letztlich aber einen abweichenden Wert besitzt im Gegensatz zur anderen Seite der Gleichung.

  

Beispielaufgabe einer widersprüchlichen Gleichung:

  

Beispielaufgabe:

Schritte zur Lösung einer linearen Gleichung:

Schritt 1: Lösen Sie auf beiden Seiten Klammern und Brüche auf und fassen Sie jeweils gleichartige Glieder zusammen:

  

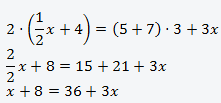
Schritt 2: Addieren/ Subtrahieren Sie so, dass alle Variablen auf der linken Seite und alle absoluten Werte auf der rechten Seite (oder umgekehrt) stehen und zusammengefasst werden können:

 

Schritt 3: Multiplizieren/ Dividieren Sie so, dass die Variable isoliert wird. Falls sich hierbei 0=0 ergibt, so ist die Gleichung eine Identitätsgleichung, die für alle  Werte  gilt.

Falls die linke von der rechten Seite verschieden ist, dann ist die ursprüngliche Gleichung widersprüchlich und damit ohne Lösung:

                                

 

Schritt 4:     Zur Probe kann das Ergebnis in die Ausgangsgleichung eingesetzt werden:

 

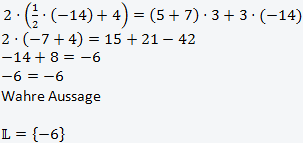
Lösungsmenge

Die Menge aller Lösungen einer Gleichung wird meist als sog. Lösungsmenge in der folgenden Form angegeben: