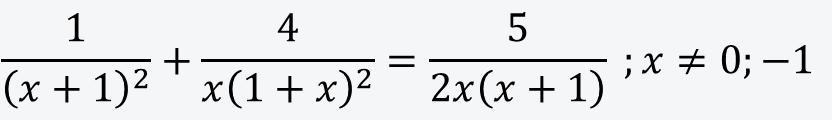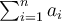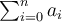Interaktives Buch
| Sitio: | iLearn - Lernmanagementsystem der Hochschule Deggendorf |
| Curso: | vhb Demo: Mathematik I |
| Libro: | Interaktives Buch |
| Imprimido por: | Invitado |
| Día: | viernes, 6 de marzo de 2026, 09:11 |
1. Rechenregeln mit reellen Zahlen -Arithmetik

Inhalt des Videos: Unterkapitel 1
Dieser Beitrag ist sehr wörtlich entnommen aus Franz Pfuff, Mathematik für Wirtschaftswissenschaftler 1, 3. Aufl, vieweg, 1995, S. 21-25.
"Jede natürliche Zahl ist interessant. Denn angenommen es gäbe eine uninteressante natürliche Zahl. Dann gäbe es auch eine kleinste uninteressante Zahl. Dies macht diese Zahl wirklich interessant! Also ist dies doch eine interessante Zahl. Dieser Widerspruch zeigt, dass es keine uninteressante Zahl gibt."

Die Menge IR der reellen Zahlen ist so konstruiert, dass in ihr die Ausführungen der vier Grundrechenarten möglich ist. Für je zwei Zahlen a, b ∈ R ist also auch
Addition a + b ∈ IR
Subtraktion a – b ∈ IR
Multiplikation a * b ∈ IR
Division (für b ≠ 0) a / b ∈ IR

Der umgekehrte Vorgang zum Ausmultiplizieren von Klammern ist das sogenannte Ausklammern, d.h. es wird aus einer Summe ein gemeinsamer Faktor der Summanden herausgezogen.
a * b + a * c = a * (b + c)
Um die Darstellung einer Summe oder eines Produktes von endlich vielen Zahlen zu vereinfachen, benützt man häufig die Symbole ∑ (Sigma) und Π (Pi).
1.1. Das Summenzeichen

Inhalt des Videos: Unterkapitel 1.1

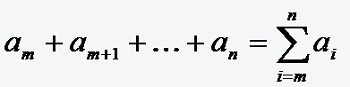
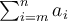 stellt also eine Anweisung dar, die Summe der Zahlen ai zu bilden, wobei i alle ganzen Zahlen von m bis n durchläuft.
stellt also eine Anweisung dar, die Summe der Zahlen ai zu bilden, wobei i alle ganzen Zahlen von m bis n durchläuft. 
a1=4, a2=7, a3=12, a4=18
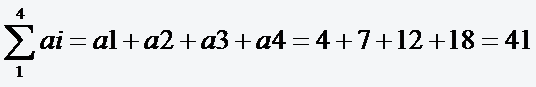

Bemerkung:
Eine größere Bedeutung hat das Summenzeichen, wenn es möglich ist, die zu summierende Größe ai explizit als eine Funktion des Summationsindex i darzustellen. Für das Erkennen von Gesetzmässigkeiten in Zahlenfolgen, die aufaddiert werden, empfiehlt sich folgende Faustregel:
1.Unterscheiden sich die Folgeglieder um gleichen Betrag (habe er den Wert d), dann ist der Ausdruck etwas mit i*d (wobei i der Laufindex ist), z.B. 2+5+8+11; hier ist gleiche Differenz 3, also ist Formel 3*i, nun geht es mit Startwert los. Starte ich mit i=1, so wäre 1*3=1 und 1 zu hoch, also muss ich meinen Ausdruck, wenn ich mit i=1 starte um 1 reduzieren. Formel lautet Summe i=1 bis 4 von 3*i-1
2. Kann ich Regel 1) nicht anwenden, zerlege ich jeden Summanden um zu sehen, dass sich die zerlegten Teile je Summand um 1 in den Bestandteilen erhöhen, z.B. 4+9+16+25 Ich zerlege 2*2+3*3+4*4+5*5 also je Summand werden die zwei Faktoren des Produktes um 1 größer, genau das mach ja auch der Summationsindex i, starte ich mit i=2 wäre i*i der erste Summand 2*2 und dann steigt i auf 3 und der zweite Summand wäre 3*3, so dass ich habe: Summe I=2 bis 5 von i*i
3. Das Vorzeichenalternieren bei den Summanden lässt sich mit (-1)i realisieren ((-1)^1=-1;(-1)^2=1; i(-1)^3=-1; (-1)^4=1), wobei man die Potenz i so variieren muss (i, i+1), so dass der erste Summand das richtige Vorzeichen hat, z.B. 1,-2,3,-4 benötigt (-1)i-1, da erstes positiv sein muss und wenn i bei 1 beginnt muss zwei als Potenz beim ersten Summanden raus kommen.

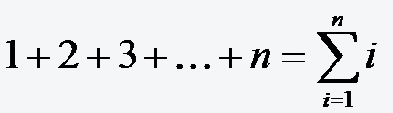

Hierbei lautet das allgemeine Bildungsgesetz:

Ungerade Zahlen kann man darstellen durch die Formel (2i-1); einen Vorzeichenwechsel durch die Formel (-1)i+1

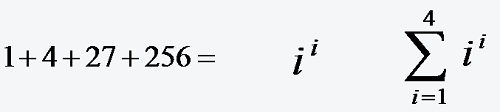

Inhalt des Videos: Unterkapitel 1.1

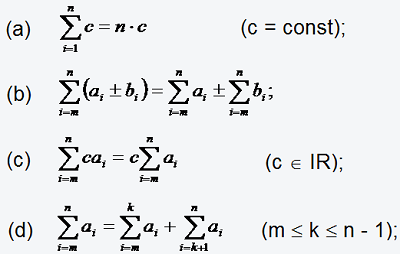
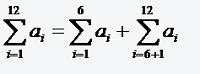
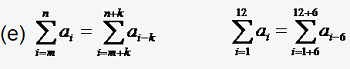
Bei vielen für die Praxis wichtigen Problemen treten doppelt indizierte Summanden aij auf. In diesem Falle kann man eine so genannte Doppelsumme bilden, indem man über beide Indices summiert.

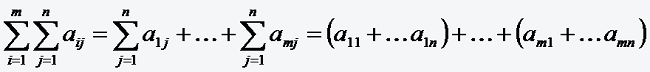


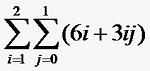
6*1+3*1*1+
6*2+3*2*1=

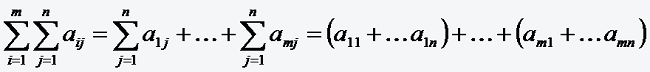
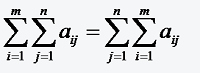
1.2. Das Produktzeichen

Inhalt des Videos: Unterkapitel 1.2

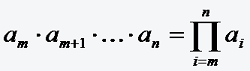
Für eine beliebige reelle Zahl bezeichnen wir an als die n-te Potenz von a. Dabei heißt a Basis und die Hochzahl n Exponent.
Wir wollen nun noch kurz die aus der Arithmetik bekannten Rechenregeln für Potenzen wiederholen.

Schreiben sie mit Hilfe des Produktzeichens
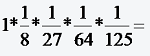
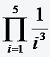
8=2*2*2
Bemerkungen: Rechenregeln
-
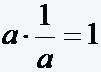 für alle beliebigen Werte von a außer der Null. Wir nennen den
für alle beliebigen Werte von a außer der Null. Wir nennen den 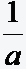 Kehrwert von a.
Kehrwert von a. -
Bei einem Bruch werden Zähler und Nenner so behandelt, wie wenn sie in Klammern stünden.
-
Zwei Brüche
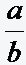 und
und  (b,y ≠ 0) werden multipliziert, indem man die Zähler miteinander und die Nenner miteinander multipliziert:
(b,y ≠ 0) werden multipliziert, indem man die Zähler miteinander und die Nenner miteinander multipliziert:
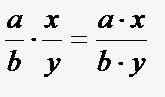
-
Der Kehrwert eines Bruchs
 ist der Bruch
ist der Bruch  .
. -
Zwei Brüche
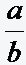 und
und  (b,y≠0) werden dividiert, indem man den Zählerbruch (bruch1) mit dem Kehrwert des Nennerbruchs (bruch2) multipliziert:
(b,y≠0) werden dividiert, indem man den Zählerbruch (bruch1) mit dem Kehrwert des Nennerbruchs (bruch2) multipliziert:
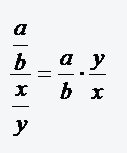
-
Kann man einen Bruch
 mit Hilfe eines Wertes c so umformen, dass man
mit Hilfe eines Wertes c so umformen, dass man 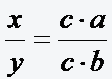 erhält, kann man den Bruch mit c kürzen und erhält
erhält, kann man den Bruch mit c kürzen und erhält 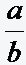 . Der Wert des neuen Bruches hat sich nicht verändert.(b, y, c ≠ 0 und c ≠ 1) . Es gilt dann also
. Der Wert des neuen Bruches hat sich nicht verändert.(b, y, c ≠ 0 und c ≠ 1) . Es gilt dann also
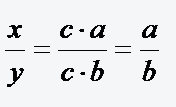
-
Brüche werden so addiert:
-
Die Brüche werden gleichnamig gemacht. Es werden also alle Brüche durch Erweitern so umgeformt, dass sie den gleichen Nenner N(N ≠ 0) haben.
-
Die Zähler, die durch das Gleichnamig-Machen resultierten, werden addiert zur Summe Z .
-
Im Ergebnis steht im Zähler die Summe Z und im Nenner der gleichnamige Ausdruck
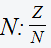 .
.
-
Eine Potenz ist ein Term, der in der Form xa dargestellt werden kann, wobei x im Allgemeinen größer als 0 und a beliebig sind.
-
Bei ungeradzahligem n (n ∈ ℕ) kann auch aus negativen Zahlen die n-te Wurzel gezogen werden.

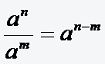 für a ≠ 0; 23/24=8/16=1/2
für a ≠ 0; 23/24=8/16=1/2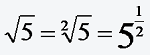
Quadratische Gleichung
•ax² + bx + c = 0
mit a, b, c ∈ IR und a ≠ 0
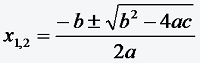
Im Falle von b² - 4ac < 0 existiert keine reellwertige Lösung.

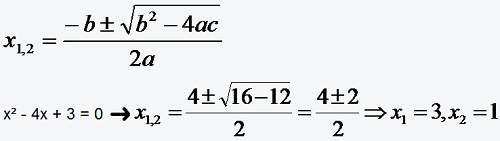
1.3. Binomkialkoeffizient und Fakultät
 Inhalt des Videos: Unterkapitel 1.3 und 1.4.
Inhalt des Videos: Unterkapitel 1.3 und 1.4.
Man bezeichnet


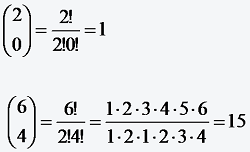

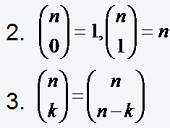

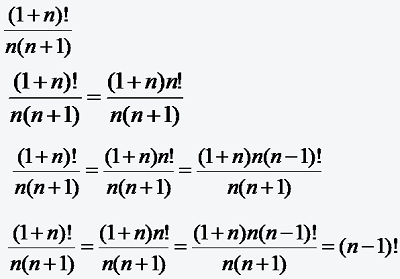
Mit Hilfe der Binomialkoeffizienten ist es außerdem möglich, einen Ausdruck der Form (a + b)n „auszumultiplizieren“, d.h. in eine Summe zu entwickeln wie folgt:

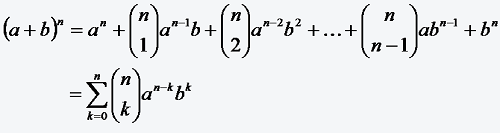

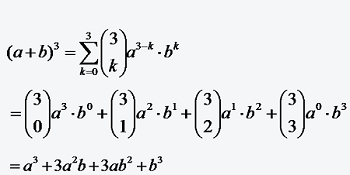
1.4. Logarithmus naturalis (ln)
 Inhalt des Videos: Unterkapitel 1.3 und 1.4.
Inhalt des Videos: Unterkapitel 1.3 und 1.4.
Logarithmen sind in der Wissenschaft ein unverzichtbares Werkzeug, denn damit können beispielsweise sehr komplizierte Formeln in einfachere Ausdrücke überführt werden.

Einführungsbeispiel:
Betrachten wir die Gleichung 5x=125 . Wir suchen den Wert x , der die Gleichung löst. Salopp könnte man das schreiben als
5?=125
Die kleine Kopfrechnung 1·5=5; 5·5=25; 5·5·5=125 verrät uns, dass
53=125
ist. Wir können die Lösung so hinschreiben
log5 125= 3
und so sprechen: „Der Logarithmus zur Basis 5 von 125 ist 3“.
Es sind die beiden Aussagen 53=125 und log5 125= 3 äquivalent, was „gleichwertig“ heißt.
„Der Logarithmus zur Basis a von y ist x .“
Der Logarithmus gibt an, welche Potenz x die Gleichung ax=y ergibt a?=y: .

Beispiele:
4?=64 → 43=64, also log464=3 .
Spezieller Logarithmus zur Basis e , wobei diese die eulersche Zahl e≈2,72 ist.
y = ex ↔ logey = x = ln y
Wir nennen ihn den natürlichen Logarithmus. Seine Kurzschreibweise ist ln y .
Die Bezeichnung natürlich hat sich eingebürgert, weil dieser Logarithmus - wie die Basis e - sehr einfach in der Anwendung ist. So findet er ähnliche Anwendungen wie e, beispielsweise bei Wachstumsprozessen. Allerdings kann man hier nicht ohne Taschenrechner auf das zugrunde liegende y schließen.

Rechenregeln für Logarithmen
Die Rechenregeln gelten für alle Basen e.
- Der Logarithmus von y ist nur für Werte y>0 definiert.
- ln 1=0
- ln (y*z)=ln y + ln z
Wir interessieren uns für ln (5·30) . Es ist ln (5·30)= ln 150 = 5,01 oder aber mit ln 5 = 1,61 und ln 30 = 3,40 :
ln (5·30)= ln 5 + ln 30 = 1,61 + 3,40 = 5,01
- ln(y/x) = ln( y)- ln(x)

Beispiel:
Wir interessieren uns für ln(528/22). Es ist ln(528/22)=ln(24)=1,38.
ln(528/22)=ln 528-ln 22=2,72-1,34=1,38
- ln (1/y)= -ln y
- ln zb= b ln z

Beispiel:
ln 153=ln 3375 = 3,5283
3 ln 15=3*1,1761=3,5283
- Eine Rechenregel, die einem das Auflösen von Gleichungen sehr erleichtern kann, ist
ln ex =x



Wir beachten: Der Ausdruck ln e bedeutet nicht ln·e , sondern er bedeutet ln(e) , also der Logarithmus von e .
Zusammenfassend können wir feststellen, dass die Rechenregeln für Logarithmen dem Umgang mit Potenzen entsprechen. Logarithmen können nur die oben beschriebenen Regeln. Ausdrücke wie ln(x+y) dürfen daher nicht weiter zerlegt werden - auch, wenn uns das manchmal unbefriedigend erscheint.
ln(x+y)<>ln(x)+ln( y )
2. Aufgaben

Aufgabe 0
Lösen Sie folgende Klammer auf:
(a + b - c) * d

Interaktive Aufgabe zu Aufgabe 0
 Lösungsvideo der Aufgabe 0:
Lösungsvideo der Aufgabe 0:

Aufgabe 1
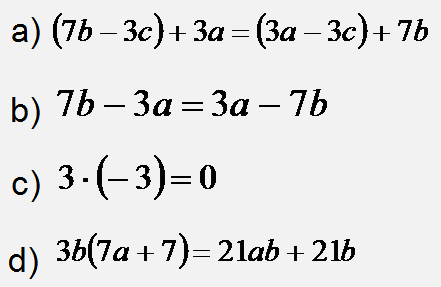

Interaktive Aufgabe zu Aufgabe 1

Aufgabe 2

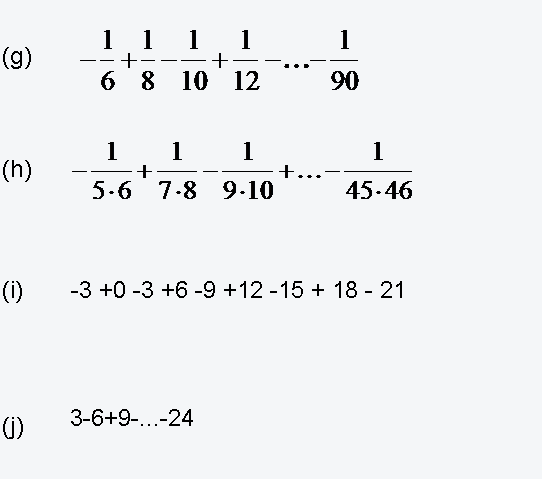


Interaktive Aufgabe zu Aufgabe 2
 Lösungsvideo der Aufgabe 2:
Lösungsvideo der Aufgabe 2:

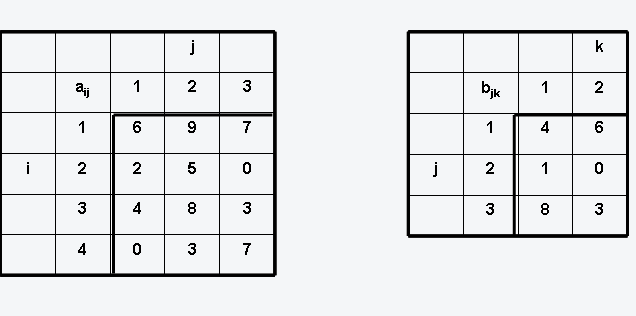
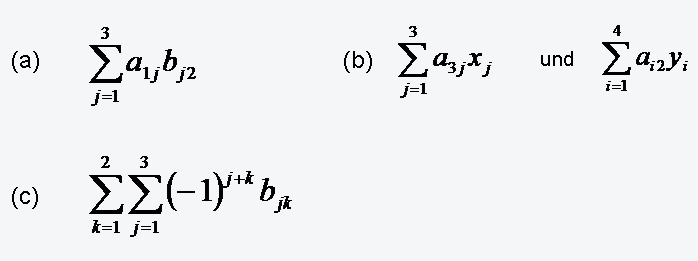

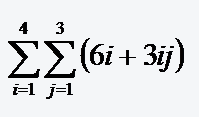

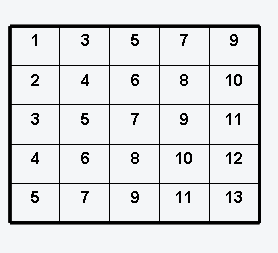
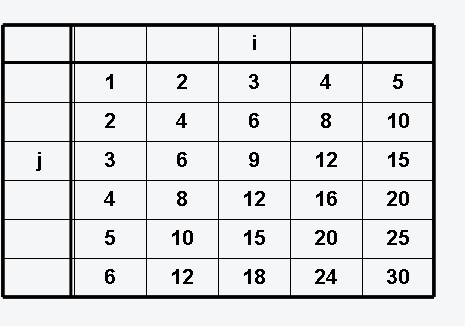
(a) Die Summe der Elemente auf der Hauptdiagonalen!
(b) Die Summe der Elemente oberhalb der Hauptdiagonalen!
(c) Die Summe der Elemente von der zweiten bis zur vierten Zeile (Spalte)
(d) Die Summe aller Elemente

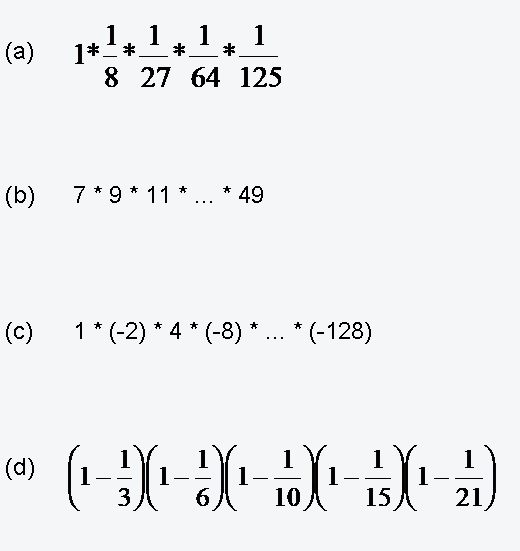

Interaktive Aufgabe zu Aufgabe 6
 Lösungsvideo der Aufgabe 6:
Lösungsvideo der Aufgabe 6:

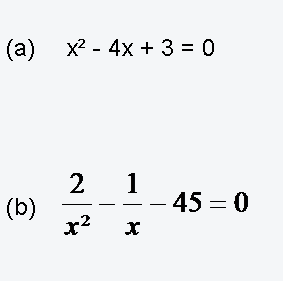

Interaktive Aufgabe zu Aufgabe 7
 Lösungsvideo der Aufgabe 7:
Lösungsvideo der Aufgabe 7:

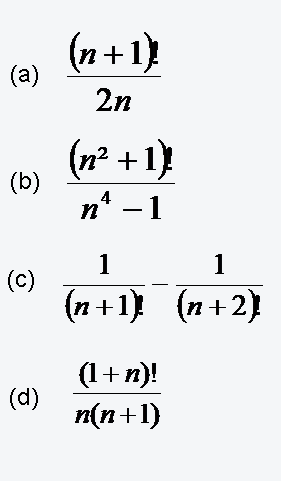

Interaktive Aufgabe zu Aufgabe 8
 Lösungsvideo der Aufgabe 8:
Lösungsvideo der Aufgabe 8:

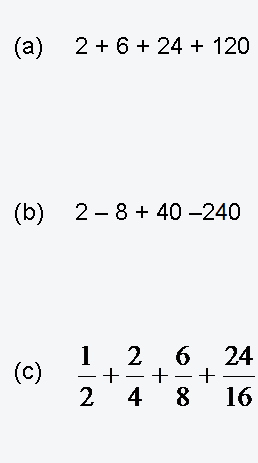
 Lösungsvideo der Aufgabe 9:
Lösungsvideo der Aufgabe 9:

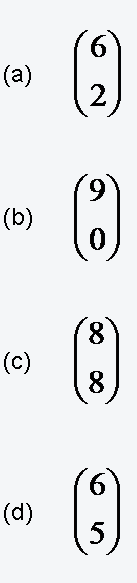

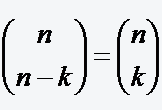


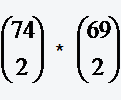
 Lösungsvideo der Aufgabe 13:
Lösungsvideo der Aufgabe 13:

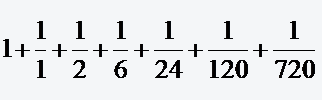

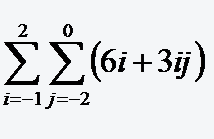

Interaktive Aufgabe zu Aufgabe 15
 Lösungsvideo der Aufgabe 15:
Lösungsvideo der Aufgabe 15:



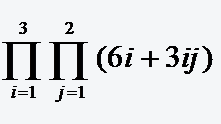

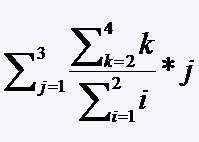

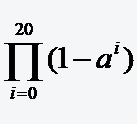
 Lösungsvideo der Aufgabe 20:
Lösungsvideo der Aufgabe 20:

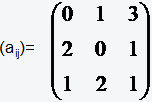
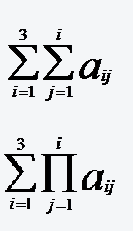
 Lösungsvideo der Aufgabe 22:
Lösungsvideo der Aufgabe 22:

Man ermittle den Wert der folgenden Summe!
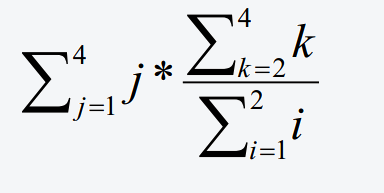
 Lösungsvideo der Aufgabe 23:
Lösungsvideo der Aufgabe 23:

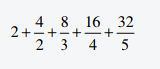

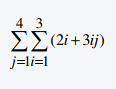

Aufgabe 26
Schreiben sie die Formel (Barwert zukünftiger Zahlungen bei veränderlichen Zinssätzen) in ausführlicher Form hin!
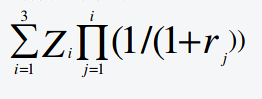

Gegeben sei die Matrix
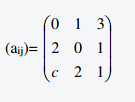
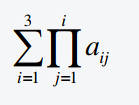

Bestimmen Sie x mit Logarithmus:
a) 10x =100.000
b) 2x = 132
 Lösungsvideo der Aufgabe 28:
Lösungsvideo der Aufgabe 28:

Aufgabe 29
Vereinfachen Sie:
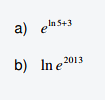
 Lösungsvideo der Aufgabe 29:
Lösungsvideo der Aufgabe 29:

Aufgabe 31
Vereinfachen Sie:
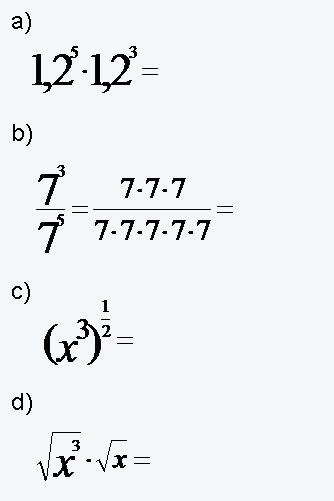

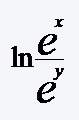

Interaktive Aufgabe zu Aufgabe 32
 Lösungsvideo der Aufgabe 32:
Lösungsvideo der Aufgabe 32: