Kapitel 2 - Einführung in die Wahrscheinlichkeitsrechnung
2.11 Unabhängige Ereignisse
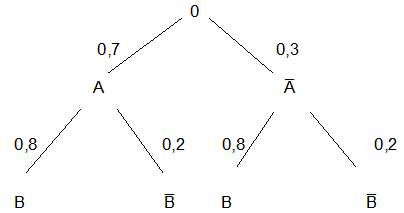
Wir gehen jetzt von folgenden Wahrscheinlichkeiten aus, ebenfalls für die Zufriedenheit von Hotelgästen (B und B̅) in Zusammenhang mit dem Geschlecht (A und
A̅).
|
Wir erkennen, dass die beiden bedingten Verteilungen (in der zweiten Ebene) gleich sind. Offensichtlich ist die Beurteilung des Hotelzimmers unabhängig davon, ob ein Gast männlich oder weiblich ist. |
|
Zunächst nehmen wir für diesen Fall die Berechnungen nach Regel (4) vor:
Nun lässt sich zusätzlich die Wahrscheinlichkeit für das Ereignis B (zufrieden) errechnen.
Es ist die Summe der ersten und dritten Wahrscheinlichkeit, die Summe der Wahrscheinlichkeiten für B jeweils „in Kombination“ mit der Bedingung „männlich“ (Ereignis A) sowie „weiblich“ (Ereignis Ā).
Wir erhalten:
P(B) = 0,56 + 0,24 = 0,80.
Damit lässt sich auch die Gültigkeit der obigen Regel (5) beispielhaft zeigen:
P(A ⋂ B) = P(A) . P(B) = 0,7 . 0,8 = 0,56.
Die unbedingte Wahrscheinlichkeit für die „Zufriedenheit“ P(B) von 0,8 ist identisch mit den bedingten Wahrscheinlichkeiten P(B|A) = 0,8 bzw. P(B|Ā).
Allgemein gilt, dass zwei Ereignisse dann unabhängig sind, wenn die Regel (5) zur Anwendung kommt!
 |
|---|