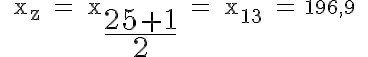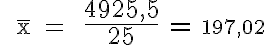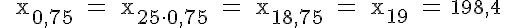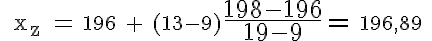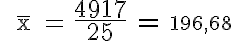Kapitel 9 - Lageparameter
| Website: | iLearn - Lernmanagementsystem der Hochschule Deggendorf |
| Kurs: | vhb Demo: Statistik I |
| Buch: | Kapitel 9 - Lageparameter |
| Gedruckt von: | Gast |
| Datum: | Samstag, 31. Januar 2026, 11:10 |
9.1 Lernziele
In diesem Kapitel lernen Sie
- welches die wichtigsten Lageparameter sind
- wie Lageparameter berechnet und interpretiert werden
-
welche Lageparameter bei welchen Daten verwendet werden können.
 |
|---|
9.2 Statistische Fragestellung
Wie lässt sich die Interpretation einer Häufigkeitsverteilung verbessern, wenn Kennzahlen für die Lage der Verteilung ermittelt werden?
Lageparameter sollen für die Datenreihe möglichst „repräsentativ“ sein und die Lage der Werte auf der Merkmalsachse charakterisieren.
Als Lageparameter finden Verwendung
- Modus (Modalwert) oder häufigster Wert: Das kann ein einziger Wert sein oder es sind mehrere Werte.
- Median oder Zentralwert: Dieser "mittlere" Wert teilt die Verteilung in die unteren bzw. oberen 50 Prozent der Merkmalsträger, d.h. er halbiert die Verteilung.
- Arithmetisches Mittel: Das ist der allgemein bekannte Durchschnittswert.
- Geometrisches Mittel: Dieser Mittelwert bezieht sich meist auf zeitliche Datenreihen und will deren durchschnittliche Entwicklung (Zunahme oder Abnahme) wiedergeben.
 |
|---|
9.3 Modus (Modalwert)
Der Modus bzw. Modalwert wurde bereits beispielhaft verwendet (siehe Kapitel 6, 7 und 8).
Für den Modus, den häufigsten Wert einer Verteilung, gelten die folgenden Formeln, wobei der Laufindexwert M die Ausprägung bzw. Klasse des Modalwerts bezeichnet:
|
nicht-klassierte Verteilung |
|
|
klassierte Verteilung |
|
|
wobei |
|
Beispiel: Lebensdauer von Ventilen
|
|
|||||||||||||||
 |
|---|
9.4 Zentralwert (Median) und Quantile
(1) Zentralwert
- Urliste
Im Falle einer ungeraden Anzahl von Beobachtungswerten ist
Im Fall einer geraden Anzahl n von Beobachtungswerten genügt jeder Wert im Intervall
![\mathsf{\Large{ \left[x_{\LARGE{\frac{n}{2}}} ; x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}} \mathsf{\Large{ \left[x_{\LARGE{\frac{n}{2}}} ; x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}}](https://ilearn.th-deg.de/filter/tex/pix.php/a77acf523536c602d53ebc0fa4c55de1.png)
der obigen Definition. Man bestimmt der Einfachheit halber die Intervallmitte als Näherungswert des Zentralwerts
Beispiel: Lebensdauer von Ventilen nach der Größe geordnet
| Beobachtung i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Dauer in Std. xi | 210 | 230 | 240 | 260 | 280 | 330 | 350 | 360 | 370 | 380 | 390 | 400 | 420 | 440 | 460 | 480 |
Welche Lebensdauer wird von 50 Prozent der Ventile erreicht oder unterschritten?
Der Zentralwert liegt zwischen 360 und 370 und beträgt (gemäß der obigen Näherungsformel) 365.
→ Die Hälfte der beobachteten Ventile hat eine Lebensdauer von 365 Stunden und weniger.
- Häufigkeitsverteilung:
Im Fall einer Häufigkeitsverteilung ist der Zentralwert der Wert, bei dem die absolute kumulierte Häufigkeit den Wert n/2 bzw. die relative kumulierte Häufigkeit den Wert von 0,5 bzw. 50 Prozent erreicht oder erstmals überschreitet.
Bei einer klassierten Häufigkeitsverteilung kann der Zentralwert innerhalb der Klasse, in der der Zentralwert liegt, durch lineare Interpolation mit Hilfe der absoluten oder relativen kumulierten Häufigkeiten ermittelt werden. (Der Index Z bezeichnet die Klasse, in der der Zentralwert liegt.)
Beispiel: Lebensdauer von Ventilen
|
[aj; bj[ |
fj |
Fj |
|
200 - 300 |
5 |
5 |
|
300 - 400 |
7 |
12 |
|
400 - 500 |
4 |
16 |
|
Summe |
16 |
Welche Lebensdauer wird von 50% der Ventile erreicht oder unterschritten?
→ Der Zentralwert liegt in der Klasse 300 – 400
Innerhalb dieser Klasse wird linear interpoliert:
→ Mindestens 50 Prozent der Ventile erreicht eine Lebensdauer von 342,86 Stunden und weniger und mindestens 50 Prozent der Ventile hat eine Lebensdauer von 342,86 Stunden und mehr.
(2) Quantile
Das Prinzip für die Ermittlung des Zentralwerts lässt sich verallgemeinern, wenn man an Stelle der 50 % Grenze andere Prozentsätze verwendet. Allgemein spricht man dann von den Quantilen einer Verteilung. Die allgemeine Definition für die Quantile lautet:
Ein p % Quantil ist dadurch charakterisiert, dass mindestens p % der Beobachtungen einen Wert kleiner gleich und mindestens (1 – p) % einen Wert größer oder gleich dem Wert xp annehmen.
Insbesondere die Quartile mit 25 % bzw. 75 % werden in der Praxis häufig verwendet, ebenso die Dezile, insbesondere das unterste 10 % Dezil und das oberste 90 % Dezil.
So besagt z.B. der oberste 90% Dezilwert, dass z.B. mindestens 90 Prozent der Bevölkerung eine Körpergröße von maximal x90 cm erreicht und mindestens 10% der Bevölkerung eine Körpergröße hat, die gleich oder größer x90 cm ist.
 |
|---|
9.5 Arithmetisches Mittel
Das arithmetische Mittel wird unter Verwendung der Urliste bzw. der Häufigkeitsverteilung wie folgt berechnet (siehe auch die entsprechenden Abschnitte in den Kapiteln 6 und 7):
Beispiel: Lebensdauer von Ventilen
| Beobachtung i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Summe |
| Dauer in Std. xi |
280 |
330 |
260 |
440 |
420 |
240 |
480 |
360 |
460 |
400 |
230 |
210 |
350 |
370 |
380 |
390 |
5600 |
Wie hoch ist die durchschnittliche Lebensdauer?
Das arithmetische Mittel beträgt 350.
Die beobachteten Ventile hatten im Durchschnitt eine Lebensdauer von 350 Stunden.
Schwerpunkteigenschaft des arithmetischen Mittels
Die Summe der Abweichungen vom arithmetischen Mittel bzw. der Durchschnitt d dieser Abweichungen ist gleich 0:
Das arithmetische Mittel liegt demnach so zentral in einer Verteilung, dass sich positive und negative Abweichungen der Merkmalswerte in der Summe ausgleichen. Deshalb werden bei der Berechnung der durchschnittlichen absoluten Abweichung die Differenzen zwischen den Merkmalswerten und dem Lageparameter absolut genommen.
Für eine Beobachtungsreihe mit den Werten 3, 6, 10, 11, 13 und 14 und dem arithmetischen Mittel von 9,5 gilt somit:
Bei klassierten Daten ist der exakte Wert von ![]() nicht zu ermitteln; man berechnet ersatzweise das gewogene arithmetische Mittel aus Klassenmitten mit den Klassenhäufigkeiten als Gewichte (siehe Lektion 7).
nicht zu ermitteln; man berechnet ersatzweise das gewogene arithmetische Mittel aus Klassenmitten mit den Klassenhäufigkeiten als Gewichte (siehe Lektion 7).
Beispiel: Lebensdauer von Ventilen
|
[aj; bj[ |
fj |
mj |
fjmj |
|
200 - 300 |
5 |
250 |
1250 |
|
300 - 400 |
7 |
350 |
2450 |
|
400 - 500 |
4 |
450 |
1800 |
|
Summe |
16 |
5500 |
Wie hoch ist die durchschnittliche Lebensdauer?
Das aus Klassenmitten errechnete arithmetische Mittel beträgt 343,75, d.h. die Ventile hatten im Durchschnitt eine Lebensdauer von etwa 343,75 Stunden.
 |
|---|
9.6 Geometrisches Mittel
Bestehen die Merkmalswerte aus Wachstumsraten, Wachstumsfaktoren oder
Zinsfaktoren, die über eine Folge von Perioden hinweg beobachtet werden, ist als Durchschnittswert
das geometrische Mittel zu verwenden.
Das geometrische Mittel ist definiert als:
Die gebräuchlichsten Anwendungen des geometrischen Mittels finden sich in der Berechnung der durchschnittlichen Wachstumsrate bzw. der Durchschnittsverzinsung.
Beispiel mehrjährige Verzinsung
Ein Bundesschatzbrief mit einer Laufzeit von sieben Jahren werde beginnend mit dem ersten Jahr zu folgenden Zinssätzen verzinst:
|
Zins rt : |
2,5 % |
3,0 % |
3,5 % |
4,25 % |
4,5 % |
5,0 % |
5,0 % |
Wie hoch ist die Durchschnittsverzinsung?
Zunächst müssen die Zinssätze rt über die Beziehungen 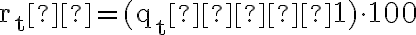 in Zinsfaktoren umgerechnet werden:
in Zinsfaktoren umgerechnet werden:
|
Zinsfaktor qt : |
1,025 |
1,03 |
1,035 |
1,0425 |
1,045 |
1,05 |
1,05 |
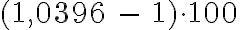 pro Jahr.
pro Jahr.
Das geometrische Mittel hat die Eigenschaft, über n Perioden hinweg denselben Effekt zu erzielen wie die sukzessive Multiplikation der n Werte.
Hier folgt ein
- Lehrvideo: Geometrisches Mittel
 |
|---|
9.7 Vergleich und Verwendung der Lageparameter
Je nach Merkmalsart bzw. Skalenniveau
einer Variablen können unterschiedliche
Lageparameter verwendet werden.
Sehen Sie selbst - durch Klicken auf Beispiel:
| Skalierung | nominal | ordinal | metrisch |
| Modus | ja Beispiel | ja Beispiel | ja Beispiel |
| Median | nein | ja Beispiel | ja Beispiel |
| arithmetisches Mittel | nein | nein | ja1) Beispiel |
Anwendungsbeispiele |
|||
| Skalierung | nominal | ordinal | metrisch |
| Modus | |||
| Median | nein | ||
| Arithmetisches Mittel | nein | nein2) | |
Anmerkungen:
1) Ausnahme: Bei Wachstumsfaktoren wird das geometrische Mittel verwendet.
2) Es ist gebräuchlich, Notendurchschnitte zu errechnen. Hier behandelt man die Note wie ein metrisch skaliertes Merkmal. Dies unterstellt allerdings, dass die Abstände zwischen den einzelnen Noten gleich groß, also "gleichwertig" sind.
Hier sehen Sie ein
- Lehrvideo: Lageparameter und Säulendiagramm
 |
|---|
9.8 Übungen
Übungsaufgaben
Sie erhalten eine Liste von 25 Tankstellen in der näheren Umgebung mit den Preisen in Euro-Cent für Benzin :
| 193,9 | 193,9 | 194,4 | 194,4 | 195,9 | 195,9 | 195,9 | 195,9 | 195,9 | 196,9 | 196,9 | 196,9 | |
| 196,9 | 196,9 | 197,9 | 197,9 | 197,9 | 197,9 | 198,4 | 198,4 | 198,9 | 198,9 | 198,9 | 199,9 | 199,9 |
Bitte beantworten Sie die folgenden Fragen und vollziehen Sie die Berechnungen nach:
|
Welcher Benzinpreis kommt am häufigsten vor? |
|
|
Welcher Benzinpreis wird von der Hälfte der Tankstellen erreicht oder unterschritten? |
|
|
Welchen Benzinpreis verlangen die Tankstellen im Durchschnitt? |
|
|
Welcher Benzinpreis wird von 3/4 aller Tankstellen erreicht oder unterschritten? |
Erstellen Sie aus diesen Messergebnissen ausgehend von 192 Cent und einer Klassenbreite von 2 Cent eine Häufigkeitsverteilung und bestimmen Sie die Lageparameter anhand dieser Häufigkeitsverteilung.
|
Welche Lageparameter ergeben sich aufgrund der Häufigkeitsverteilung? |
Übungsvideo: Lageparameter - Klassierte Häufigkeitsverteilung
Optionale Übungen (nicht klausurrelevant)
Die nachfolgenden Excel-Dateien bieten ergänzende Übungsmöglichkeiten, wobei zur vollständigen Bearbeitung die Aktivierung der Excel-Makrofunktion erfolgen muss.
Hinweis: Excel für APPLE bietet die Makrofunktion leider nicht an.
 |
|---|
9.9 Kontrollfragen
- der Modus, Modalwert oder häufigste Wert?
- der Modalwert einer klassierten Häufigkeitsverteilung?
- die Vorgehensweise bei der Berechnung des Arithmetischen Mittels?
- der Median oder Zentralwert?
- das Geometrische Mittel?
Mauszeiger auf die Frage: Die Antwort erscheint.
 |
|---|
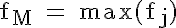
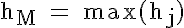
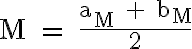
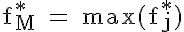
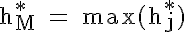
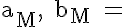
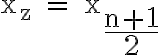
![\mathsf{\Large{x_z = \frac{1}{2} \left[x_{\LARGE {\frac{n}{2}}} + x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}} \mathsf{\Large{x_z = \frac{1}{2} \left[x_{\LARGE {\frac{n}{2}}} + x_{\LARGE{\frac{n}{2}} \Large {+1}}\right]}}](https://ilearn.th-deg.de/filter/tex/pix.php/466d489219add38dd129aff6961702f8.png)
![\mathsf{\Large{x_z = \frac{1}{2}\left[\normalsize{360+370}\right] = \normalsize{365}}} \mathsf{\Large{x_z = \frac{1}{2}\left[\normalsize{360+370}\right] = \normalsize{365}}}](https://ilearn.th-deg.de/filter/tex/pix.php/0743ec73a9c0d60800aad2155ecc7063.png)
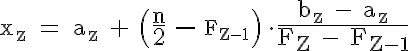
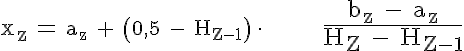
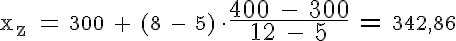
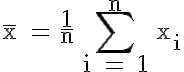
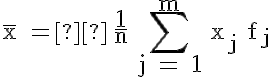
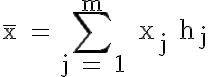
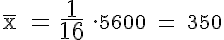
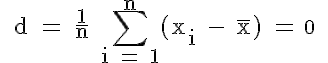
![\mathsf{ F(M) = \Large {\frac{1}{6}} \normalsize {\left[ (3 - 9,5) + (6 - 9,5) + (10 - 9,5) + (11 - 9,5) + (13 - 9,5) + (14 - 9,5)\right] = 0 }} \mathsf{ F(M) = \Large {\frac{1}{6}} \normalsize {\left[ (3 - 9,5) + (6 - 9,5) + (10 - 9,5) + (11 - 9,5) + (13 - 9,5) + (14 - 9,5)\right] = 0 }}](https://ilearn.th-deg.de/filter/tex/pix.php/09bae0756005a78c06718d7f1e78b592.png)
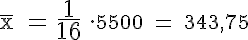
![\mathsf{ \large{ G = \sqrt[\LARGE{n}]{\strut \large {x_1\cdot x_2\cdot ... \cdot x_n} } } } \mathsf{ \large{ G = \sqrt[\LARGE{n}]{\strut \large {x_1\cdot x_2\cdot ... \cdot x_n} } } }](https://ilearn.th-deg.de/filter/tex/pix.php/dab5956170857487cbb60725c3a594c4.png)
![\mathsf{ \large{ G = \sqrt[\LARGE{7}]{\strut \normalsize {1,025\cdot 1,03\cdot 1,035\cdot 1,0425\cdot 1,045\cdot 1,05\cdot 1,05}} = \sqrt[\LARGE{7}]{\strut \normalsize {1,3124}} = \normalsize {1,0396} }} \mathsf{ \large{ G = \sqrt[\LARGE{7}]{\strut \normalsize {1,025\cdot 1,03\cdot 1,035\cdot 1,0425\cdot 1,045\cdot 1,05\cdot 1,05}} = \sqrt[\LARGE{7}]{\strut \normalsize {1,3124}} = \normalsize {1,0396} }}](https://ilearn.th-deg.de/filter/tex/pix.php/2032138824a11f7a1f2d4b3b582461a3.png)