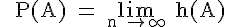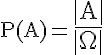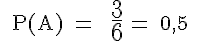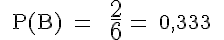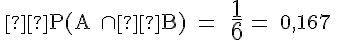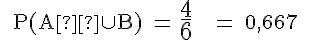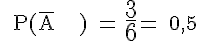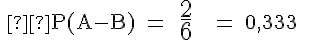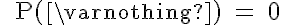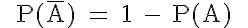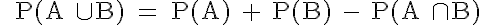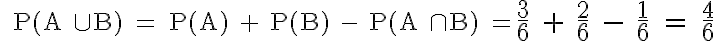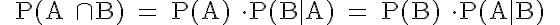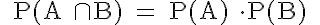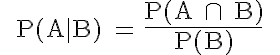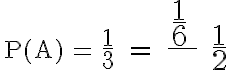Kapitel 2 - Einführung in die Wahrscheinlichkeitsrechnung

2.1 Lernziele

In diesem Kapitel lernen Sie

die Regeln für die Durchführung eines Zufallsexperiments
den Unterschied von Ergebnissen und Ereignissen
die grundlegenden Formeln und Rechenregeln für die Wahrscheinlichkeit
die bedingte Wahrscheinlichkeit.

	Glossar

2.2 Zufallsexperiment

Um von einem Zufallsexperiment sprechen zu können, müssen wir Folgendes beachten:

Das Experiment ist - gedanklich oder tatsächlich - unter gleichen Bedingungen beliebig oft wiederholbar.

Es wird nach bestimmten Regeln durchgeführt.

Das Ergebnis lässt sich nicht mit Sicherheit vorhersagen.

Die bekanntesten Zufallsexperimente sind:

der Würfelwurf		der Münzwurf
das Ziehen von Karten		das Ziehen von Kugeln (Lottozahlen)

Eine der Grundregeln für ein Zufallsexperiment ist das Mischen der Spielkarten bzw. Kugeln. Diese Regel soll dafür sorgen, dass in der Ziehungs-Gesamtheit keine Regelmäßigkeit von Karten bzw. Kugeln vorhanden ist.

Die zweite Regel betrifft das „blinde“ oder „ verdeckte“ Ziehen von Kugeln oder Karten.

Und schließlich müssen mindestens zwei unterschiedliche Ergebnisse bei der Ziehung möglich sein.

Alle Zufallsexperimente lassen sich als Ziehung von Kugeln aus einer Urne abbilden, dem sogenannten Urnenmodell (siehe Abschnitt 2.3).

	Glossar

2.3 Urnenmodell

Von einem Urnenmodell sprechen wir, wenn in einer Urne (z.B. einem Gefäß oder einer Lostrommel) eine bestimmte Anzahl von Kugeln liegt und eine oder mehrere dieser Kugeln herausgenommen werden.

Festzulegen sind bei einer Ziehung von Kugeln nach dem Urnenmodell:

Eigenschaften der Urne: Anzahl Kugeln, Art der Kugeln

Ziehungsumfang: Anzahl der zu entnehmenden Kugeln

Ziehungsvorschrift: mit oder ohne Zurücklegen

Ergebnisdarstellung: mit oder ohne Beachtung der Reihenfolge

Auf Basis dieser Festlegungen können folgende Zufallsexperimente als Urnenmodell beschrieben werden:

	Würfel	Münze	Skatspiel	Lottoziehung
Urne - Anzahl N Kugeln - Art der Kugeln	6 1, 2, 3, 4, 5, 6	2 Kopf, Zahl	32 Herz, Ass, 10, ...	49 1, 2, ..., 49
Ziehungsumfang Anzahl n	z.B. 2	z.B. 5	z.B. 4	z.B. 6
Ziehungsvorschrift	mit Zurücklegen	mit Zurücklegen	ohne Zurücklegen	ohne Zurücklegen
Beachtung der Reihenfolge	im allg. ohne	im allg. ohne	ohne	ohne

	Glossar

2.4 Ergebnisse und Ereignisse

Wir sehen uns den Unterschied zwischen Ergebnissen und Ereignissen am Würfelbeispiel an.

Ergebnis	mögliches Resultat eines Zufallsexperiments (1-mal Würfeln) Augenzahl 1, 2, 3, 4, 5 oder 6
Ereignisraum bzw. Ergebnismenge (Ω)	Menge aller möglichen Ergebnisse eines Zufallsexperiments {1, 2, 3, 4, 5, 6} als Ereignisraum Ω
Ereignis (A)	Teilmenge des Ereignisraumes Bsp.: A bedeutet gerade Augenzahlen: 2, 4, 6
Elementarereignis	Ereignis, das aus einem einzigen Element/Ergebnis besteht Bsp.: die Augenzahl 5: {5}

Zur Veranschaulichung des Beispiels "Würfelwurf" können Sie sich in Abschnitt 2.7 ein Lehrvideo ansehen.

	Glossar

2.5 Verknüpfung von Ereignissen

Ereignisse können analog zu Mengenoperationen miteinander verknüpft werden.

Gehen wir von den folgenden drei Ereignissen des Würfelbeispiels aus:

Ereignis A = gerade Augenzahlen: {2, 4, 6}
Ereignis B = Augenzahlen kleiner gleich 2: {1, 2}
Ereignis C = Augenzahl 5: {5}

Die drei grundlegenden Verknüpfungsmöglichkeiten ergeben als

- "Produkt"

- "Summe"

- "Differenz"

A ∩ B = {2}

A U B = {1, 2, 4 ,6}

A - B = {4, 6}

die Schnittmenge von A und B.

die Vereinigungsmenge von A und B.

die Menge A ohne die Elemente von B.

Das Komplementärereignis Ā entspricht der Menge „außerhalb“ des ursprünglichen Ereignisses:

Ā = {1, 3, 5} d.h. die ungeraden Zahlen.

Disjunkte Ereignisse sind Ereignisse, deren Schnittmenge leer ist: A ∩ C = {ø}

	Glossar

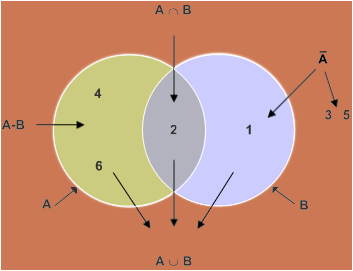
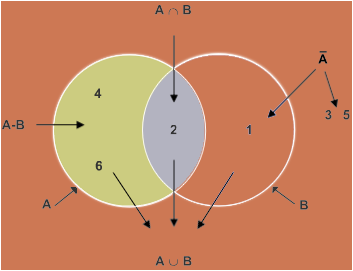
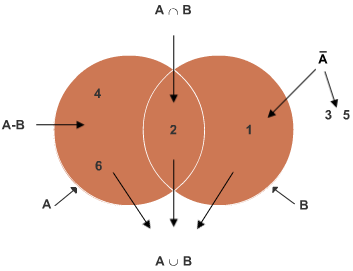
2.6 Venn-Diagramm

Das Venn-Diagramm stellt Ereignisse und ihre Verknüpfungen als Mengen in Form von Flächen grafisch dar.

Beispiel für Ω = {1, 2, 3, 4, 5, 6} eines Würfels mit A {gerade Zahlen} und B {Zahlen kleiner gleich 2}

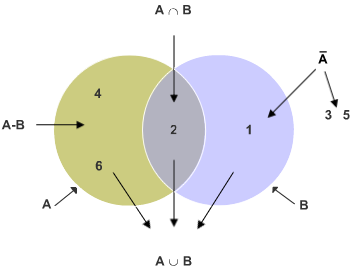Die Grundregeln der Wahrscheinlichkeitsrechnung beziehen sich auf das unmögliche Ereignis , das Komplementärereignis und die Vereinigung von Ereignissen.

Antwort: Mauszeiger auf die Begriffe (Mouseover)

	Glossar

2.7 Wahrscheinlichkeitsbegriffe

Es gibt drei verschiedene Begriffe für die Definition der Wahrscheinlichkeit:

Statistische Wahrscheinlichkeit
Klassische Wahrscheinlichkeit (nach Laplace)
Axiomatische Wahrscheinlichkeit (nach Kolmogoroff).

(1) Die statistische Wahrscheinlichkeit

Die statistische Wahrscheinlichkeit P(A) ist derjenige Wert, bei dem sich die relative Häufigkeit h(A) bei einer zunehmenden Zahl von Zufallsexperimenten stabilisiert:

$\mathsf{ \normalsize{ P(A) = \lim\limits_{n \to \infty} h(A) } }$

(2) Die klassische Wahrscheinlichkeit

Die klassische oder mathematische Wahrscheinlichkeit ist der Quotient aus der Anzahl der für das Ereignis A günstigen Fälle und der Anzahl aller möglichen Fälle:

$\mathrm{ \normalsize{ P(A) =\Large{ \frac{|A|}{|\Omega|} } } }$

Wir ermitteln die Wahrscheinlichkeiten für die 6 im nachfolgenden Venn-Diagramm angegebenen Ereignisse.

Bei Ω = {1, 2, 3, 4, 5, 6} des Würfels ergeben sich:

$\mathsf{ \normalsize{ P(A) = \Large{ \frac{3}{6} }\normalsize{= 0,5 } }}$ $\mathsf{ \normalsize{ P(B) = \Large{ \frac{2}{6} }\normalsize{= 0,333 } }}$ $\mathsf{ \normalsize{ P(A \cap B) =\Large{ \frac{1}{6} }\normalsize{= 0,167 } }}$

$\mathsf{ \normalsize{ P(A \cup B) = \Large{\frac{4}{6} } \normalsize{ = 0,667 }} }$ $\mathsf{ \normalsize{ P(\overline{A} ) = \Large {\frac{3}{6}} \normalsize{= 0,5 } } }$ $\mathsf{ \normalsize{ P(A-B) =\Large{ \frac{2}{6} } \normalsize{ = 0,333 } }}$

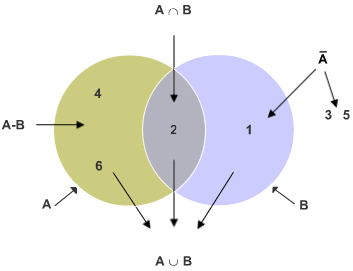(3) Die axiomatische Wahrscheinlichkeit

Axiom 1

Jedem Ereignis A ist eine reelle Zahl größer gleich 0 und kleiner gleich 1 zugeordnet, die Wahrscheinlichkeit P(A) heißt:

0 ≤ P(A) ≤ 1

Axiom 2

Die Wahrscheinlichkeit für das sichere Ereignis ist gleich 1,0:

P(Ω) = 1

Axiom 3

Die Wahrscheinlichkeit für das Vereinigungsereignis zweier disjunkter Ereignisse ist die Summe der beiden Wahrscheinlichkeiten:

P(A U B) = P(A) + P(B), wenn P(A ∩ B) = ø

Die axiomatische Wahrscheinlichkeit am Würfelbeispiel Kap3_Würfel

zu Axiom 1: P(A) = 0,5 das entspricht 50%

zu Axiom 2: Die Wahrscheinlichkeit, eine 1, 2, 3, 4, 5 oder 6 zu werfen, ist 1 bzw. 100%

zu Axiom 3: A und A̅ sind disjunkt;

Die Wahrscheinlichkeitssumme ist P(A) + P(A̅) = 0,5 + 0,5 = 1,0.

Sehen Sie hier ein Lehrvideo.

Hinweis: Mit dem Button CC können Sie die UNTERTITEL jederzeit ein- und ausschalten!

Lehrvideo: Wahrscheinlichkeitsbegriffe Würfelwurf

Kreuztabelle für verknüpfte Ereignisse

Die Kreuztabelle ist eine wichtige Darstellungsform für die Verknüpfungen von Ereignissen:

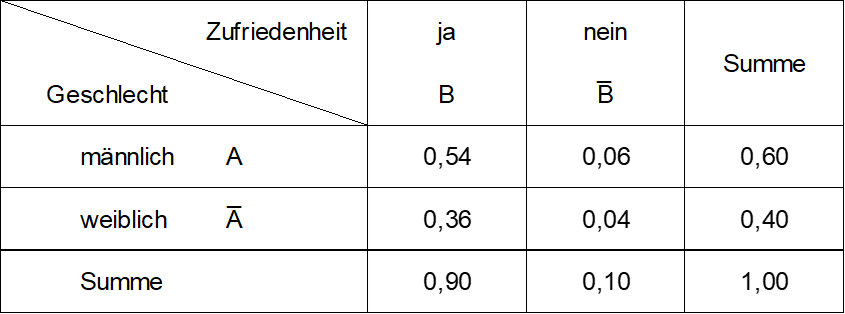
Die Kreuztabelle enthält Randwahrscheinlichkeiten und Wahrscheinlichkeiten für die kombinierten Ausprägungen.

Wir erkennen in der obigen Tabelle, dass - wegen der vorliegenden Unabhängigkeit - die Zellenwahrscheinlichkeiten als Produkte der Randwahrscheinlichkeiten zustande kommen.

	Glossar

2.8 Regeln der Wahrscheinlichkeitsrechnung

Sehen wir uns die 3 Grundregeln der Wahrscheinlichkeitsrechnung an.

Regel (1): Wahrscheinlichkeit des unmöglichen Ereignisses

$\mathsf{ \large{ P(\varnothing) = 0 } }$

Diese Regel bedeutet für das Würfelspiel, dass die Wahrscheinlichkeit für die leere Menge (z.B. für das unmögliche Ereignis, die Zahl 7 zu würfeln) gleich 0 ist.

Regel (2): Wahrscheinlichkeit des Komplementärereignisses

$\mathsf{ \large{ P(\overline{A}) = 1 - P(A) } }$

Diese Regel kann beispielsweise auf die ungeraden Zahlen bezogen werden, die das Komplementärereignis zu den geraden Zahlen sind. Wir erhalten als Komplementärwahrscheinlichkeit 0,5 = 1 - 0,5.

Regel (3): Additionssatz für beliebige Ereignisse

$\mathsf{ \large{ P(A \cup B) = P(A) + P(B) - P(A \cap B) } }$

Diese Regel betrifft die Addition zweier Ereignisse, die nicht disjunkt sind. Für unsere beiden Würfel-Ereignisse
A und B:

$\mathsf{ \large{ P(A \cup B) = P(A) + P(B) - P(A \cap B) =\Large{\frac{3}{6} + \frac{2}{6} - \frac{1}{6} = \frac{4}{6} } }}$

Das Vereinigungsereignis besteht aus den vier Elementen 2, 4, 6 und 1.

Das Ereignis „1“ aus der Schnittmenge darf nur einmal gezählt werden.

Würfelwurf

Ergänzend gibt es zwei Regeln als Multiplikationssätze.

Regel (4): Multiplikationssatz für beliebige Ereignisse

$\mathsf{ \large{ P(A \cap B) = P(A) \cdot P(B|A) = P(B) \cdot P(A|B) } }$

P(B|A) bzw. P(A|B) bezeichnen hierbei sogenannte bedingte Wahrscheinlichkeiten, die auf den folgenden Seiten erläutert werden.

Regel (5): Multiplikationssatz für unabhängige Ereignisse

$\mathsf{ \large{ P(A \cap B) = P(A) \cdot P(B) } }$

	Glossar

2.9 Bedingte Wahrscheinlichkeit

Eine bedingte Wahrscheinlichkeit P(A|B) gibt die Wahrscheinlichkeit für das Ereignis A an, unter der Bedingung, dass B bereits eingetreten ist oder eintritt oder eintreten wird.

$\mathsf{ \large{ P(A|B) = \Large{\frac{P(A\ \cap \ B)}{P(B)} } }}$

Damit wird die Anzahl der möglichen Ergebnisse von B zur Bezugsgröße und wir dividieren - analog den Wahrscheinlichkeiten - die Mächtigkeit (Anzahl Elemente) der Menge A ∩ B durch die Mächtigkeit der Menge B.

Beispiel: Würfelwurf

Wir definieren das Ereignis B „ungerade Zahlen“ und das Ereignis A „Augenzahl 5“.

Damit ergibt sich als bedingte Wahrscheinlichkeit für A unter der Bedingung B 1/3.

Wenn wir wissen, dass Ereignis B eingetreten ist - d.h. eines der möglichen Ergebnisse (1, 3, 5) -, dann ist - unter dieser Bedingung - die Wahrscheinlichkeit für A

$\mathsf{ \large{P(A)} = \Large{\frac{1}{3} = \frac{ \LARGE{\frac{1}{6} }} {\LARGE{ \frac{1}{2} }} } }$

Und hier noch ein ergänzendes

Lehrvideo: Zweidimensionale und bedingte Wahrscheinlichkeit

	Glossar

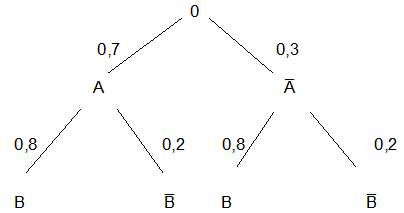
2.10 Wahrscheinlichkeitsbaum

Definition und Anwendung bedingter Wahrscheinlichkeiten können graphisch mit Hilfe eines Wahrscheinlichkeitsbaumes gezeigt werden.

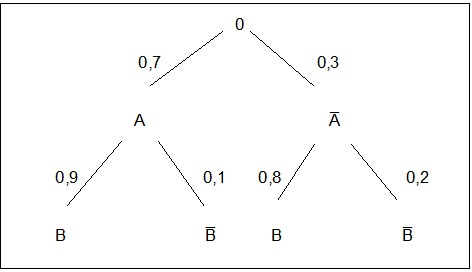
Hier werden insgesamt drei Wahrscheinlichkeitsverteilungen dargestellt.

Zunächst sehen wir die Verteilung der Variablen "Geschlecht" mit den beiden Wahrscheinlichkeiten 0,7 für „männlich“ (Ereignis A) und 0,3 für „weiblich“ (Ereignis A̅).

Dann folgen die beiden Verteilungen der Variablen „Zufriedenheit mit dem Hotelzimmer“ mit den Wahrscheinlichkeiten 0,9 und 0,1 bei den männlichen sowie 0,8 und 0,2 bei den weiblichen Hotelgästen. Hier liegen bedingte Wahrscheinlichkeiten vor. Die Wahrscheinlichkeit dafür, dass ein Gast zufrieden ist (Ereignis B), beträgt unter de r Bedingung, dass er männlich ist, 0,9 (Wahrscheinlichkeit P(B|A)) etc.

Wir können für die insgesamt vier Zweige des Wahrscheinlichkeitsbaumes die dazugehörigen Wahrscheinlichkeiten berechnen.

Es handelt sich jeweils um die Wahrscheinlichkeit des Produkts zweier Ereignisse (Multiplikationssatz Regel (4)).

P(A ∩ B) = P(A) ∙ P(B\|A) = 0,7 ∙ 0,9 =	0,63
P(A ∩ B̅) = P(A) ∙ P(B̅\|A) =0,7 ∙ 0,1 =	0,07
P(Ā ∩ B) = P(Ā) ∙ P(B\|Ā) = 0,3 ∙ 0,8 =	0,24
P(Ā ∩ B̅) = P(Ā) ∙ P(B̅\|Ā) =0,3 ∙ 0,2 =	0,06
Summe	1,0

→ P (männl. und zufr.) =	P (männl.) mal P (zufr. wenn männl.)
→ P (männl. u. unzufr.) =	P (männl.) mal P (unzufr. wenn männl.)
→ P (weibl. und zufr.) =	P (weibl.) mal P (zufr. wenn weiblich)
→ P (weibl. und unzufr.) =	P (weibl.) mal P (unzufr. wenn weibl.)

Schritt vor >>

Hier noch ein

Lehrvideo: Wahrscheinlichkeitsbaum

	Glossar

2.11 Unabhängige Ereignisse

Wir gehen jetzt von folgenden Wahrscheinlichkeiten aus, ebenfalls für die Zufriedenheit von Hotelgästen (B und B̅) in Zusammenhang mit dem Geschlecht (A und A̅).

Wir erkennen, dass die beiden bedingten Verteilungen (in der zweiten Ebene) gleich sind.

Offensichtlich ist die Beurteilung des Hotelzimmers unabhängig davon, ob ein Gast männlich oder weiblich ist.

P(A ∩ B) = P(A) ∙ P(B\|A) = 0,7 ∙ 0,8 =	0,56
P(A ∩ B̅) = P(A) ∙ P(B̅\|A) = 0,7 ∙ 0,2 =	0,14
P(Ā ∩ B) = P(Ā) ∙ P(B\|Ā) = 0,3 ∙ 0,8 =	0,24
P(Ā ∩ B̅) = P(Ā) ∙ P(B̅\|Ā) = 0,3 ∙ 0,2 =	0,06
Summe	1,0

Zunächst nehmen wir für diesen Fall die Berechnungen nach Regel (4) vor:

Nun lässt sich zusätzlich die Wahrscheinlichkeit für das Ereignis B (zufrieden) errechnen.

Es ist die Summe der ersten und dritten Wahrscheinlichkeit, die Summe der Wahrscheinlichkeiten für B jeweils „in Kombination“ mit der Bedingung „männlich“ (Ereignis A) sowie „weiblich“ (Ereignis Ā).

Wir erhalten:

P(B) = 0,56 + 0,24 = 0,80.

Damit lässt sich auch die Gültigkeit der obigen Regel (5) beispielhaft zeigen:

P(A ⋂ B) = P(A) ^. P(B) = 0,7 ^. 0,8 = 0,56.

Die unbedingte Wahrscheinlichkeit für die „Zufriedenheit“ P(B) von 0,8 ist identisch mit den bedingten Wahrscheinlichkeiten P(B|A) = 0,8 bzw. P(B|Ā).

Allgemein gilt, dass zwei Ereignisse dann unabhängig sind, wenn die Regel (5) zur Anwendung kommt!

	Glossar

2.12 Übungen

Optionale Übungen (nicht klausurrelevant)

Die nachfolgenden Excel-Dateien bieten ergänzende Übungsmöglichkeiten, wobei zur vollständigen Bearbeitung die Aktivierung der Excel-Makrofunktion erfolgen muss.

Hinweis: Excel für APPLE bietet die Makrofunktion leider nicht an.

Interaktive Übung 1: Wahrscheinlichkeit

Interaktive Übung 2: Wahrscheinlichkeitsbaum

	Glossar

2.13 Kontrollfragen

Mauszeiger auf die Frage: Die Antwort erscheint.

	Glossar

Hier kommen Sie zum

Klausurtraining Kapitel 2

zum nächsten Kapitel

	Glossar

Website:	iLearn - Lernmanagementsystem der Hochschule Deggendorf
Kurs:	vhb Demo: Statistik II
Buch:	Kapitel 2 - Einführung in die Wahrscheinlichkeitsrechnung

Gedruckt von:	Gast
Datum:	Sonntag, 19. Mai 2024, 10:48