Lektion 3 - Wahrscheinlichkeitsbegriffe und Kombinatorik
| Site: | iLearn - Lernmanagementsystem der Hochschule Deggendorf |
| Course: | vhb Demo: Statistik II (alt) |
| Book: | Lektion 3 - Wahrscheinlichkeitsbegriffe und Kombinatorik |
| Printed by: | Gast |
| Date: | Wednesday, 25 February 2026, 8:36 AM |
Description
In dieser Lektion lernen Sie,
- die Regeln für die Durchführung eines Zufallsexperiments,
- Ergebnisse und Ereignisse kennen,
- die grundlegenden Formeln und Rechenregeln für die Wahrscheinlichkeit,
- die bedingte Wahrscheinlichkeit kennen.
Table of contents
3.1 Lernziele
In dieser Lektion lernen Sie
- die drei verschiedenen Wahrscheinlichkeitsbegriffe
- die Anwendung des Satzes von Bayes
- Grundregeln der Kombinatorik kennen.
3.2 Wahrscheinlichkeitsbegriffe
Wir kennen drei verschiedene Begriffe für die Darlegung der Wahrscheinlichkeit
- Statistische Wahrscheinlichkeit
- Klassische Wahrscheinlichkeit (nach Laplace)
- Axiomatische Wahrscheinlichkeit (nach Kolmogoroff)
Die statistische Wahrscheinlichkeit
Die statistische Wahrscheinlichkeit P(A) ist derjenige Wert, bei dem sich die relative Häufigkeit h(A) bei einer zunehmenden Zahl von Zufallsexperimenten stabilisiert:
![]()
Die klassische Wahrscheinlichkeit
Die klassische oder mathematische Wahrscheinlichkeit ist der Quotient aus der Anzahl der für das Ereignis A günstigen Fälle und der Anzahl aller möglichen Fälle:
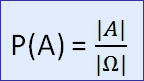
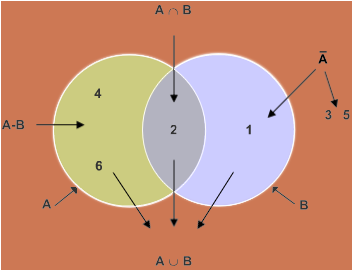
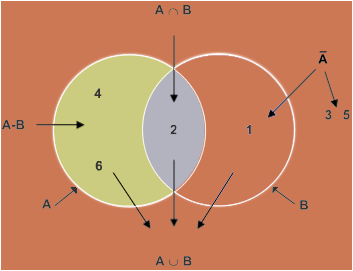
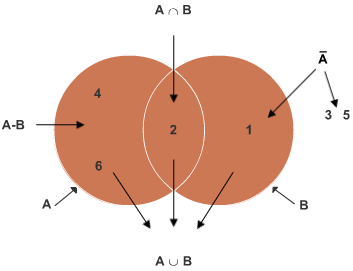
Geben Sie die sechs Wahrscheinlichkeiten für das nachfolgende Venn-Diagramm an:
Das Venn-Diagramm
...Beispiel für Ω = {1,2,3,4,5,6} eines Würfels
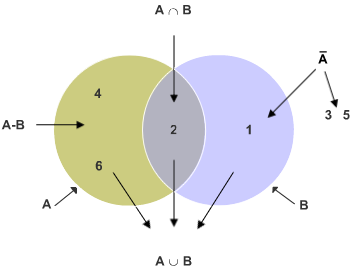 |
Die Grundregeln der Wahrscheinlichkeitsrechnung beziehen sich auf das unmögliche Ereignis, das Komplementärereignis und die Vereinigung beliebiger Ereignisse. Antwort: Mauszeiger auf die Begriffe (Mouseover) |
Die axiomatische Wahrscheinlichkeit
Axiom 1
Jedem Ereignis A ist eine reelle Zahl größer gleich 0 und kleiner gleich 1 zugeordnet, die Wahrscheinlichkeit P(A) heißt:
Axiom 2
Die Wahrscheinlichkeit für das sichere Ereignis ist gleich 1:
Axiom 3
Die Wahrscheinlichkeit für das Vereinigungsereignis zweier disjunkter Ereignisse ist die Summe der beiden Wahrscheinlichkeiten:
Die axiomatische Wahrscheinlichkeit am Würfelbeispiel
zu Axiom 1: P(A) = 0,5 das entspricht 50%
zu Axiom 2: Die Wahrscheinlichkeit, eine 1,2,3,4,5 oder 6 zu werfen, ist 1 bzw. 100%
zu Axiom 3: A und Ā sind disjunkt.
Die Wahrscheinlichkeitssumme ist 1.
Kreuztabelle für verknüpfte Ereignisse
Die Kreuztabelle ist eine wichtige Darstellungsform für die Verknüpfungen von Ereignissen:
| Zufriedenheit | ja | nein | Summe | |
| Geschlecht | B | |||
| männlich | A | 0,54 | 0,06 | 0,60 |
| weiblich | Ā | 0,36 | 0,04 | 0,40 |
| Summe | 0,90 | 0,10 | 1,00 | |
Die Kreuztabelle enthält Randwahrscheinlichkeiten und Wahrscheinlichkeiten für die kombinierten Ausprägungen.
Wir erkennen in der obigen Tabelle, dass - wegen der vorliegenden Unabhängigkeit - die Zellenwahrscheinlichkeiten als Produkte der Randwahrscheinlichkeiten zustande kommen.
3.3 Der Satz von Bayes
Der Satz von Bayes soll in diesem Kurs auf den folgenden Seiten in zwei Varianten vorgestellt werden:
Variante 1: A-priori- und A-posteriori-Wahrscheinlichkeiten
Variante 2: Die totale Wahrscheinlichkeit
3.3.1 A-priori- und A-posteriori-Wahrscheinlichkeiten
Das Ereignis, dass eine Person eine bestimmte Krankheit hat, trete mit der Wahrscheinlichkeit P(A) = 0,002 ein, d.h. 2 von 1.000 Personen haben diese Krankheit.
P(A) nennt man die A-priori-Wahrscheinlichkeit von A.
Die Wahrscheinlichkeit, dass eine Person nicht an der Krankheit A erkrankt ist, beträgt dann P(Ā) = 0,998.
In einem Test soll ermittelt werden, ob eine Person diese Krankheit hat. Das Ereignis B bedeutet dann, dass der Test positiv ausfällt - d.h. dass angezeigt wird, dass die Person die Krankheit hat.
P(B) ist die A-priori-Wahrscheinlichkeit von B.
Damit lauten die Ereignisse:
A = „krank“, Ā = „nicht krank“, B = „Test positiv“, ![]() = „Test negativ“.
= „Test negativ“.
Der pharmazeutische Anbieter des Tests garantiert, dass der Test die Krankheit mit einer Wahrscheinlichkeit von 0,99 erkennt: Damit ist P(B|A) = 0,99 und P(B|Ā) = 0,01.
Frage: Wie wahrscheinlich ist das Vorliegen einer Krankheit, wenn das Testergebnis positiv ist?
oder: Wie wahrscheinlich ist das Vorliegen keiner Erkrankung bei positivem Testergebnis = falsch positives Testergebnis?
Satz von Bayes:
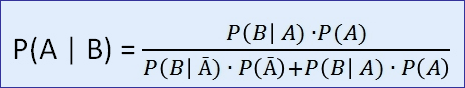
und im Beispiel:
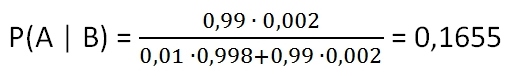
Die A-posteriori-Wahrscheinlichkeit, dass der Test „richtig positiv“ entscheidet, ist gleich 16,6%.
Damit ist die Komplementär-Wahrscheinlichkeit, dass der Test „falsch positiv“ entscheidet, erstaunlich hoch: 83,4%.
In einer Kreuztabelle (angewandt auf insgesamt 100.000 Personen) lässt sich dies wie folgt darstellen:
| Person ist... | krank | gesund | Summe | ||
| Testergebnis ist... | A | Ā | |||
| positiv | B | in % | 99,00 | 1,00 | 1,20 |
| absolut | 198 | 998 | 1.196 | ||
| negativ | in % | 1,00 | 99,00 | 99,80 | |
| absolut | 2 | 98.802 | 98.804 | ||
| Summe | in % | 0,20 | 99,80 | 100,00 | |
| absolut | 200 | 99.800 | 100.000 |
Wahrscheinlichkeit für falsch positiv (in %): 998,00 / 1.196,00 · 100 = 83,44 %
Wahrscheinlichkeit für richtig positiv (in %): 198,00 / 1.196,00 · 100 =16,56 %
3.3.2 Die totale Wahrscheinlichkeit
Besteht ein Ereignisraum aus zwei (oder mehr) Ereignissen B1, B2,... und wird zusätzlich ein beliebiges Ereignis A definiert, dann gilt als totale Wahrscheinlichkeit
![]()
Um die Anwendung des Satzes der totalen Wahrscheinlichkeit von Bayes zu zeigen, passen wir zunächst die allgemeingültige Symbolik mit beliebig vielen Ereignissen B1, B2 ,... an die obigen Beispiele an.
Setzen wir B1 gleich B und B2 gleich ![]() , dann lässt sich obige Regel in modifizierter Form darstellen:
, dann lässt sich obige Regel in modifizierter Form darstellen:

Wir können diese Formel wie folgt lesen:
Die Wahrscheinlichkeit für das Ereignis A (männlich) ist die Summe der beiden bedingten Wahrscheinlichkeiten für männlich (Bedingung B = „zufrieden“ bzw. ![]() = „unzufrieden“).
= „unzufrieden“).
Dabei werden die bedingten Wahrscheinlichkeiten mit der Wahrscheinlichkeit für zufrieden bzw. unzufrieden multipliziert.
Nehmen wir die Berechnung nun für den obigen Fall der Unabhängigkeit vor, dann setzen wir die beiden bedingten Wahrscheinlichkeiten für männlich jeweils gleich den unbedingten Wahrscheinlichkeiten von 0,7.
Als Berechnung ergibt sich damit:
P(A) = 0,7 ∙ 0,8 + 0,7 ∙ 0,2 = 0,56 + 0,14 = 0,7.
Wir erkennen, dass die Wahrscheinlichkeit nach dem Satz der totalen Wahrscheinlichkeit dadurch entsteht, dass zwei (bedingte) Wahrscheinlichkeiten „gewichtet“ addiert werden (Summe der „Gewichte“ 0,8 und 0,2 = 1,00).
3.4 Kombinatorik - Fakultät
Fakultät n!
Die Fakultät n! einer Zahl n ist das Produkt
![]()
mit 0! = 1
Die Anwendung dieser mathematischen Funktion bezieht sich in der Statistik meist auf die Anzahl der möglichen Anordnungen von n Elementen und wird üblicherweise als Anzahl von Permutationen bezeichnet.
Dazu das folgende Beispiel:
Im Regal eines Einzelhändlers sollen die 5 Warenarten A, B, C, D und E in den vorhandenen 5 Reihen untergebracht werden. Im Zusammenhang mit der Überlegung, welche Warenart in welcher Reihe die meiste Aufmerksamkeit auf sich lenkt, stellt sich die Frage, wieviele Möglichkeiten der Anordnung es überhaupt gibt.
Die Anzahl der Permutationen von 5 verschiedenen Elementen beträgt
5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 120
Dieses Ergebnis der Permutationen lässt sich leicht nachvollziehen, wenn wir uns die Möglichkeiten der Anordnungen für jeden Platz (Reihe im Regal) vorstellen.
Für die erste Reihe können alle 5 Warenarten ausgewählt werden, für die zweite Reihe die verbleibenden 4, für die dritte Reihe die übrigen 3 usw.
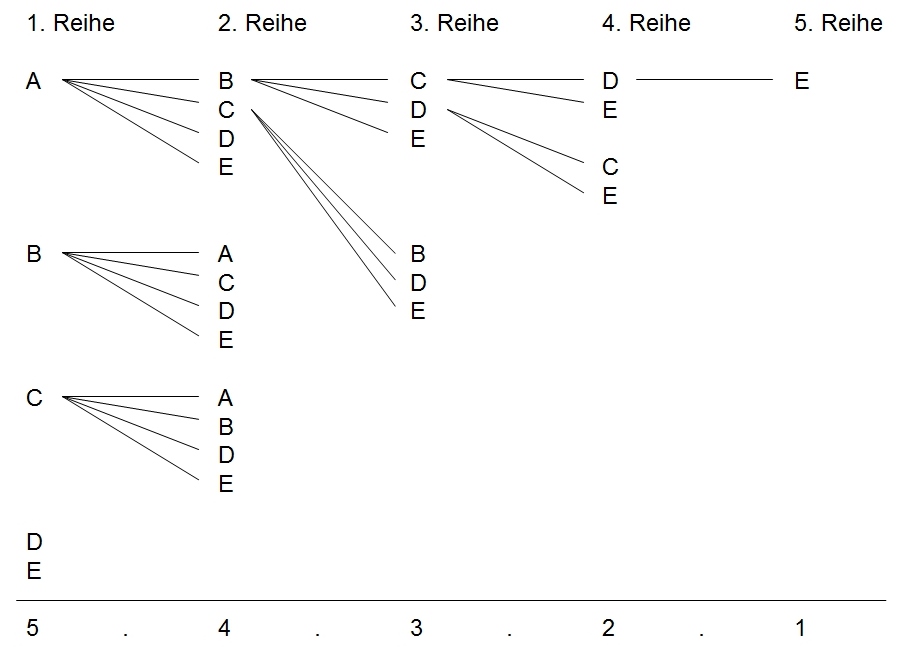
3.5 Kombinatorik - Permutationen
Die Anzahl der Anordnungen von n Elementen mit k Kategorien (mit jeweils n1, n2, ..., nk Elementen je Kategorie) beträgt:
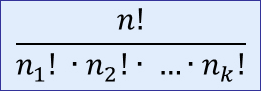
Wenn nun die n Elemente in k Kategorien aufgeteilt sind (z.B. in k = 2 Farben), dann reduziert sich die Anzahl der möglichen Anordnungen.
Wir wollen ein Beispiel wählen, das folgende Frage beantworten soll:
Wie groß ist die Anzahl der Anordnungen von 5 Elementen, von denen 3 blau (B) und 2 weiß (W) sind?
Gemäß der obigen Formel ergeben sich
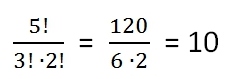
Möglichkeiten.
Es fallen (durch Division) die 3! Möglichkeiten innerhalb der ersten Kategorie und die 2! Möglichkeiten innerhalb der zweiten Kategorie weg, die bei Verschiedenheit aller Elemente noch vorlagen. Damit können wir alle 10 Möglichkeiten darstellen:

Eine ähnliche Fragestellung ergibt sich, wenn wir k Elemente mit einer bestimmten Eigenschaft auf n Plätzen anordnen wollen und uns die Anzahl der Möglichkeiten interessiert.
Hierfür verwenden wir den Binomialkoeffizienten.
Der Binomialkoeffizient
Die Anzahl der Anordnungen von k Elementen der Eigenschaft A auf n Plätzen ist:
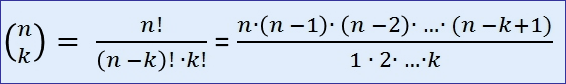
Betrachten wir als Beispiel die Anzahl der möglichen Anordnungen von k = 3 weißen Kugeln auf n = 5 Plätzen.
Dazu müssen wir zusätzlich annehmen, dass 2 Kugeln (= n-k) die Eigenschaft „nicht-weiß“ besitzen.
Nach der obigen Formel erhalten wir - wie beim obigen Bespiel der blauen und weißen Elemente - insgesamt 10 Möglichkeiten, d.h. es resultiert auch hier:
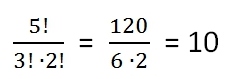
Der Binomialkoeffizient erweist sich als Spezialfall der Permutationen mit zwei Eigenschaften (= binomial).
Auf der Basis der jetzt abgeleiteten Begriffe können wir die Kombinationen definieren und die jeweilige Anzahl von Möglichkeiten diskutieren.
3.6 Kombinatorik - Kombinationen
Greifen wir aus einer statistischen Gesamtheit mit n Elementen k Elemente heraus, dann erhalten wir Kombinationen k-ter Ordnung.
Hierbei ist zu unterscheiden zwischen
der Ziehungsvorschrift
- mit und
- ohne Zurücklegen
sowie der Ergebnisdarstellung
- mit und
- ohne Beachtung der Reihenfolge
|
Kombinationen (k aus n Elementen) |
mit Beachtung der Reihenfolge |
ohne Beachtung der Reihenfolge |
| mit Zurücklegen | 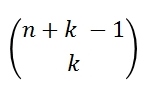 |
|
| ohne Zurücklegen | 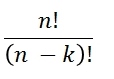 |
Wir wollen die Möglichkeiten am Beispiel einer Urne mit insgesamt 4 Kugeln und einer Ziehung von 2 Kugeln erörtern.
Bezeichnet man die Kugeln mit den Zahlen 1 bis 4, ergeben sich die folgenden Kombinationen: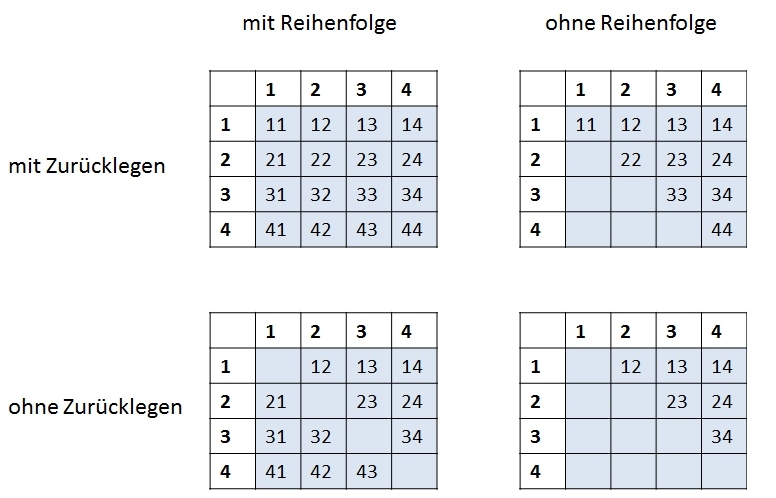
Wir haben 4 ∙ 4 = 16 Möglichkeiten vor uns, wenn wir mit Zurücklegen ziehen und die Reihenfolge beachten.
Beim Übergang auf das Modell ohne Zurücklegen fallen die Diagonalelemente weg und es verbleiben 12 Möglichkeiten.
Ziehen wir mit Zurücklegen und beachten die Reihenfolge nicht, dann ergeben sich 10 Möglichkeiten.
Und schließlich existieren nur 6 Möglichkeiten, wenn ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen wird. Diese 6 Fälle sind durch die Verschiedenheit aller Ergebnisse gekennzeichnet.
Besonders wichtig für die spätere Anwendung bei Wahrscheinlichkeitsverteilungen und Methoden sind der Fall „Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge“ bzw. der Fall „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge“.
Übungsvideo einfügen
3.7 Terminologie 1 - Wahrscheinlichkeitsbegriffe
- Was bedeutet die Wahrscheinlichkeit für das unmögliche Ereignis?
- Was bedeutet die additive Verknüpfung von Wahrscheinlichkeiten für die Ereignisse A und B?
- Was bedeutet die Wahrscheinlichkeit des Komplementärereignisses zu A?
- Was ist die multiplikative Verknüpfung von Wahrscheinlichkeiten für A und B?
- Was ist die Wahrscheinlichkeit A unter der Bedingung B?
- Wie wird die Wahrscheinlichkeit unabhängiger Ereignisse A und B berechnet?
- Wie wird die Wahrscheinlichkeit abhängiger Ereignisse A und B berechnet?
Mauszeiger auf die Frage: Die Antwort erscheint.
3.8 Terminologie 2 - Wahrscheinlichkeit und Kombinatorik
- A-priori-Wahrscheinlichkeiten
- A-posteriori-Wahrscheinlichkeiten
- Totale Wahrscheinlichkeit
- Permutationen
- Kombinationen
- Binomialkoeffizient
Mauszeiger auf die Frage: Die Antwort erscheint.
3.9 Übungen - interaktiv
Hier können Sie folgende Übungen herunterladen.
3.10 Lernvideos
Hier können Sie folgende Lernvideos sehen:
- Video - Satz von Bayes
- Video - Zweidimensionale und bedingte Wahrscheinlichkeit
- Video - Kombinatorik