Lektion 3 - Wahrscheinlichkeitsbegriffe und Kombinatorik
In dieser Lektion lernen Sie,
- die Regeln für die Durchführung eines Zufallsexperiments,
- Ergebnisse und Ereignisse kennen,
- die grundlegenden Formeln und Rechenregeln für die Wahrscheinlichkeit,
- die bedingte Wahrscheinlichkeit kennen.
3.5 Kombinatorik - Permutationen
Die Anzahl der Anordnungen von n Elementen mit k Kategorien (mit jeweils n1, n2, ..., nk Elementen je Kategorie) beträgt:
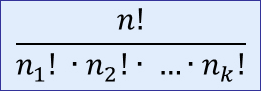
Wenn nun die n Elemente in k Kategorien aufgeteilt sind (z.B. in k = 2 Farben), dann reduziert sich die Anzahl der möglichen Anordnungen.
Wir wollen ein Beispiel wählen, das folgende Frage beantworten soll:
Wie groß ist die Anzahl der Anordnungen von 5 Elementen, von denen 3 blau (B) und 2 weiß (W) sind?
Gemäß der obigen Formel ergeben sich
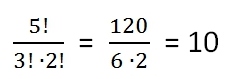
Möglichkeiten.
Es fallen (durch Division) die 3! Möglichkeiten innerhalb der ersten Kategorie und die 2! Möglichkeiten innerhalb der zweiten Kategorie weg, die bei Verschiedenheit aller Elemente noch vorlagen. Damit können wir alle 10 Möglichkeiten darstellen:

Eine ähnliche Fragestellung ergibt sich, wenn wir k Elemente mit einer bestimmten Eigenschaft auf n Plätzen anordnen wollen und uns die Anzahl der Möglichkeiten interessiert.
Hierfür verwenden wir den Binomialkoeffizienten.
Der Binomialkoeffizient
Die Anzahl der Anordnungen von k Elementen der Eigenschaft A auf n Plätzen ist:
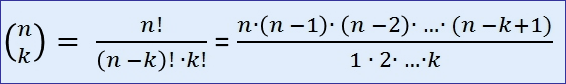
Betrachten wir als Beispiel die Anzahl der möglichen Anordnungen von k = 3 weißen Kugeln auf n = 5 Plätzen.
Dazu müssen wir zusätzlich annehmen, dass 2 Kugeln (= n-k) die Eigenschaft „nicht-weiß“ besitzen.
Nach der obigen Formel erhalten wir - wie beim obigen Bespiel der blauen und weißen Elemente - insgesamt 10 Möglichkeiten, d.h. es resultiert auch hier:
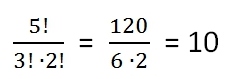
Der Binomialkoeffizient erweist sich als Spezialfall der Permutationen mit zwei Eigenschaften (= binomial).
Auf der Basis der jetzt abgeleiteten Begriffe können wir die Kombinationen definieren und die jeweilige Anzahl von Möglichkeiten diskutieren.
