Lektion 3 - Wahrscheinlichkeitsbegriffe und Kombinatorik
In dieser Lektion lernen Sie,
- die Regeln für die Durchführung eines Zufallsexperiments,
- Ergebnisse und Ereignisse kennen,
- die grundlegenden Formeln und Rechenregeln für die Wahrscheinlichkeit,
- die bedingte Wahrscheinlichkeit kennen.
3.6 Kombinatorik - Kombinationen
Greifen wir aus einer statistischen Gesamtheit mit n Elementen k Elemente heraus, dann erhalten wir Kombinationen k-ter Ordnung.
Hierbei ist zu unterscheiden zwischen
der Ziehungsvorschrift
- mit und
- ohne Zurücklegen
sowie der Ergebnisdarstellung
- mit und
- ohne Beachtung der Reihenfolge
|
Kombinationen (k aus n Elementen) |
mit Beachtung der Reihenfolge |
ohne Beachtung der Reihenfolge |
| mit Zurücklegen | 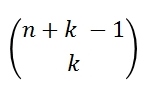 |
|
| ohne Zurücklegen | 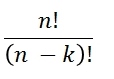 |
Wir wollen die Möglichkeiten am Beispiel einer Urne mit insgesamt 4 Kugeln und einer Ziehung von 2 Kugeln erörtern.
Bezeichnet man die Kugeln mit den Zahlen 1 bis 4, ergeben sich die folgenden Kombinationen: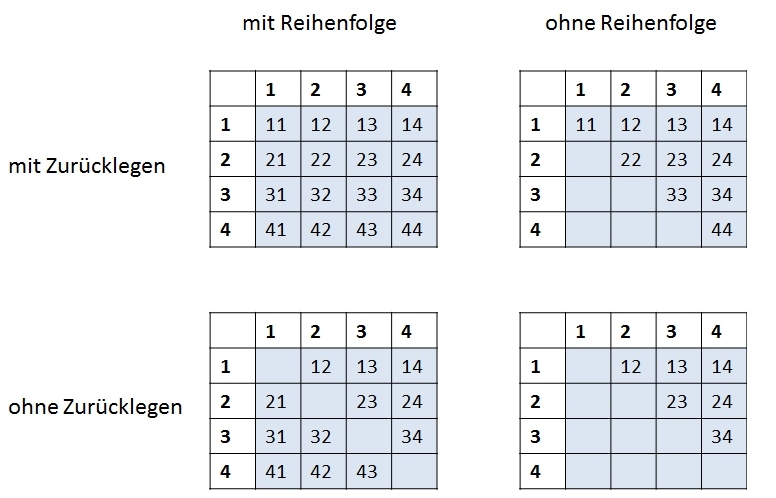
Wir haben 4 ∙ 4 = 16 Möglichkeiten vor uns, wenn wir mit Zurücklegen ziehen und die Reihenfolge beachten.
Beim Übergang auf das Modell ohne Zurücklegen fallen die Diagonalelemente weg und es verbleiben 12 Möglichkeiten.
Ziehen wir mit Zurücklegen und beachten die Reihenfolge nicht, dann ergeben sich 10 Möglichkeiten.
Und schließlich existieren nur 6 Möglichkeiten, wenn ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen wird. Diese 6 Fälle sind durch die Verschiedenheit aller Ergebnisse gekennzeichnet.
Besonders wichtig für die spätere Anwendung bei Wahrscheinlichkeitsverteilungen und Methoden sind der Fall „Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge“ bzw. der Fall „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge“.
Übungsvideo einfügen
