Interaktives Buch
1. Rechenregeln mit reellen Zahlen -Arithmetik
1.2. Das Produktzeichen

Inhalt des Videos: Unterkapitel 1.2

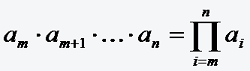
Für eine beliebige reelle Zahl bezeichnen wir an als die n-te Potenz von a. Dabei heißt a Basis und die Hochzahl n Exponent.
Wir wollen nun noch kurz die aus der Arithmetik bekannten Rechenregeln für Potenzen wiederholen.

Schreiben sie mit Hilfe des Produktzeichens
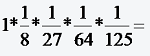
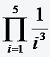
8=2*2*2
Bemerkungen: Rechenregeln
-
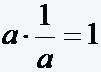 für alle beliebigen Werte von a außer der Null. Wir nennen den
für alle beliebigen Werte von a außer der Null. Wir nennen den 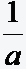 Kehrwert von a.
Kehrwert von a. -
Bei einem Bruch werden Zähler und Nenner so behandelt, wie wenn sie in Klammern stünden.
-
Zwei Brüche
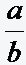 und
und  (b,y ≠ 0) werden multipliziert, indem man die Zähler miteinander und die Nenner miteinander multipliziert:
(b,y ≠ 0) werden multipliziert, indem man die Zähler miteinander und die Nenner miteinander multipliziert:
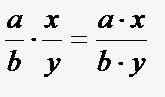
-
Der Kehrwert eines Bruchs
 ist der Bruch
ist der Bruch  .
. -
Zwei Brüche
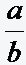 und
und  (b,y≠0) werden dividiert, indem man den Zählerbruch (bruch1) mit dem Kehrwert des Nennerbruchs (bruch2) multipliziert:
(b,y≠0) werden dividiert, indem man den Zählerbruch (bruch1) mit dem Kehrwert des Nennerbruchs (bruch2) multipliziert:
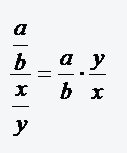
-
Kann man einen Bruch
 mit Hilfe eines Wertes c so umformen, dass man
mit Hilfe eines Wertes c so umformen, dass man 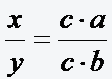 erhält, kann man den Bruch mit c kürzen und erhält
erhält, kann man den Bruch mit c kürzen und erhält 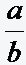 . Der Wert des neuen Bruches hat sich nicht verändert.(b, y, c ≠ 0 und c ≠ 1) . Es gilt dann also
. Der Wert des neuen Bruches hat sich nicht verändert.(b, y, c ≠ 0 und c ≠ 1) . Es gilt dann also
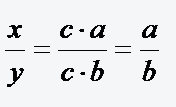
-
Brüche werden so addiert:
-
Die Brüche werden gleichnamig gemacht. Es werden also alle Brüche durch Erweitern so umgeformt, dass sie den gleichen Nenner N(N ≠ 0) haben.
-
Die Zähler, die durch das Gleichnamig-Machen resultierten, werden addiert zur Summe Z .
-
Im Ergebnis steht im Zähler die Summe Z und im Nenner der gleichnamige Ausdruck
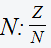 .
.
-
Eine Potenz ist ein Term, der in der Form xa dargestellt werden kann, wobei x im Allgemeinen größer als 0 und a beliebig sind.
-
Bei ungeradzahligem n (n ∈ ℕ) kann auch aus negativen Zahlen die n-te Wurzel gezogen werden.

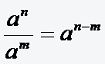 für a ≠ 0; 23/24=8/16=1/2
für a ≠ 0; 23/24=8/16=1/2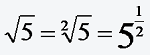
Quadratische Gleichung
•ax² + bx + c = 0
mit a, b, c ∈ IR und a ≠ 0
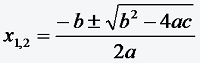
Im Falle von b² - 4ac < 0 existiert keine reellwertige Lösung.