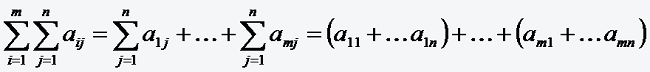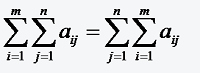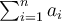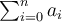Interaktives Buch
1. Rechenregeln mit reellen Zahlen -Arithmetik
1.1. Das Summenzeichen

Inhalt des Videos: Unterkapitel 1.1

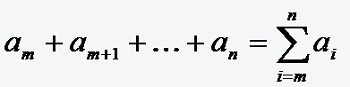
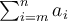 stellt also eine Anweisung dar, die Summe der Zahlen ai zu bilden, wobei i alle ganzen Zahlen von m bis n durchläuft.
stellt also eine Anweisung dar, die Summe der Zahlen ai zu bilden, wobei i alle ganzen Zahlen von m bis n durchläuft. 
a1=4, a2=7, a3=12, a4=18
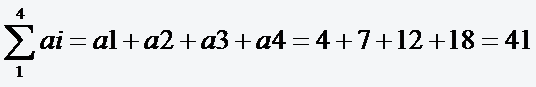

Bemerkung:
Eine größere Bedeutung hat das Summenzeichen, wenn es möglich ist, die zu summierende Größe ai explizit als eine Funktion des Summationsindex i darzustellen. Für das Erkennen von Gesetzmässigkeiten in Zahlenfolgen, die aufaddiert werden, empfiehlt sich folgende Faustregel:
1.Unterscheiden sich die Folgeglieder um gleichen Betrag (habe er den Wert d), dann ist der Ausdruck etwas mit i*d (wobei i der Laufindex ist), z.B. 2+5+8+11; hier ist gleiche Differenz 3, also ist Formel 3*i, nun geht es mit Startwert los. Starte ich mit i=1, so wäre 1*3=1 und 1 zu hoch, also muss ich meinen Ausdruck, wenn ich mit i=1 starte um 1 reduzieren. Formel lautet Summe i=1 bis 4 von 3*i-1
2. Kann ich Regel 1) nicht anwenden, zerlege ich jeden Summanden um zu sehen, dass sich die zerlegten Teile je Summand um 1 in den Bestandteilen erhöhen, z.B. 4+9+16+25 Ich zerlege 2*2+3*3+4*4+5*5 also je Summand werden die zwei Faktoren des Produktes um 1 größer, genau das mach ja auch der Summationsindex i, starte ich mit i=2 wäre i*i der erste Summand 2*2 und dann steigt i auf 3 und der zweite Summand wäre 3*3, so dass ich habe: Summe I=2 bis 5 von i*i
3. Das Vorzeichenalternieren bei den Summanden lässt sich mit (-1)i realisieren ((-1)^1=-1;(-1)^2=1; i(-1)^3=-1; (-1)^4=1), wobei man die Potenz i so variieren muss (i, i+1), so dass der erste Summand das richtige Vorzeichen hat, z.B. 1,-2,3,-4 benötigt (-1)i-1, da erstes positiv sein muss und wenn i bei 1 beginnt muss zwei als Potenz beim ersten Summanden raus kommen.

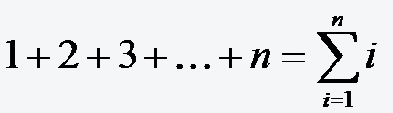

Hierbei lautet das allgemeine Bildungsgesetz:

Ungerade Zahlen kann man darstellen durch die Formel (2i-1); einen Vorzeichenwechsel durch die Formel (-1)i+1

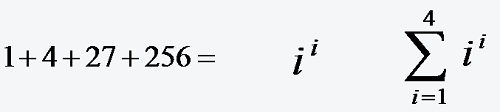

Inhalt des Videos: Unterkapitel 1.1

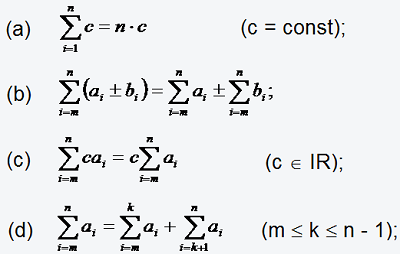
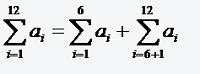
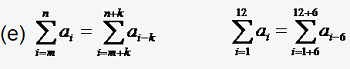
Bei vielen für die Praxis wichtigen Problemen treten doppelt indizierte Summanden aij auf. In diesem Falle kann man eine so genannte Doppelsumme bilden, indem man über beide Indices summiert.

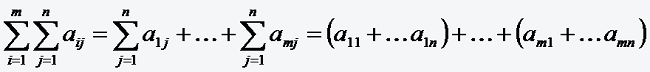


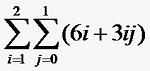
6*1+3*1*1+
6*2+3*2*1=