Interaktives Buch
Abschlussbedingungen
1. Rechenregeln mit reellen Zahlen -Arithmetik
1.3. Binomkialkoeffizient und Fakultät
 Inhalt des Videos: Unterkapitel 1.3 und 1.4.
Inhalt des Videos: Unterkapitel 1.3 und 1.4.
(1.4.6) Definition
Seien n, k ∈ N ∪ {0} mit k ≤ n. Dann setzen wir
(a)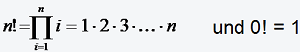
(sprich: n- Fakultät);
n! ist die Anzahl der möglichen Anordnungen
(b)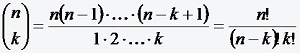
(sprich: n über k).
Man bezeichnet
Binomialkoeffizient n über k ist Anzahl der k-elementigen Teilmengen aus einer n-elementigen Menge.

Beispiele
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
71!= am Taschenrechner nicht rechenbar (69! ist die letzte rechenbare Zahl).

Beispiele
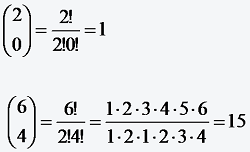

(1.4.7) Satz
Für die Zahlen n, k ∈ N mit k ≤ n gilt:
1. (n + 1)! = (n + 1) * n! z.B 4! = 4*3!
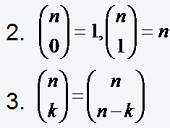

Beispiel:
Vereinfachen sie folgenden Ausdruck:
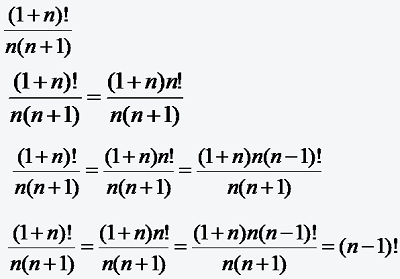
Mit Hilfe der Binomialkoeffizienten ist es außerdem möglich, einen Ausdruck der Form (a + b)n „auszumultiplizieren“, d.h. in eine Summe zu entwickeln wie folgt:

(1.4.8) Satz
Seien a, b ∈ IR und n ∈ N. Dann gilt:
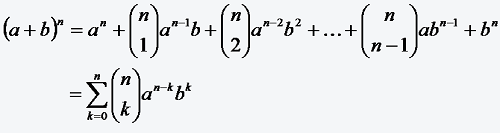

Beispiel: