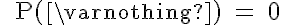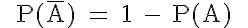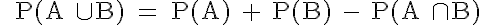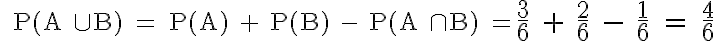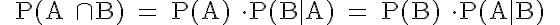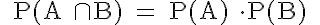Kapitel 2 - Einführung in die Wahrscheinlichkeitsrechnung
2.8 Regeln der Wahrscheinlichkeitsrechnung
Sehen wir uns die 3 Grundregeln der Wahrscheinlichkeitsrechnung an.
Regel (1): Wahrscheinlichkeit des unmöglichen Ereignisses
Diese Regel bedeutet für das Würfelspiel, dass die Wahrscheinlichkeit für die leere Menge (z.B. für das unmögliche Ereignis, die Zahl 7 zu würfeln) gleich 0 ist.
Regel (2): Wahrscheinlichkeit des Komplementärereignisses
Diese Regel kann beispielsweise auf die ungeraden Zahlen bezogen werden, die das Komplementärereignis zu den geraden Zahlen sind. Wir erhalten als Komplementärwahrscheinlichkeit 0,5 = 1 - 0,5.
Regel (3): Additionssatz für beliebige Ereignisse
Diese Regel betrifft die Addition zweier Ereignisse, die nicht disjunkt sind. Für unsere beiden Würfel-Ereignisse
A und B:
Das Vereinigungsereignis besteht aus den vier Elementen 2, 4, 6 und 1.
Das Ereignis „1“ aus der Schnittmenge darf nur einmal gezählt werden.

Ergänzend gibt es zwei Regeln als Multiplikationssätze.
Regel (4): Multiplikationssatz für beliebige Ereignisse
P(B|A) bzw. P(A|B) bezeichnen hierbei sogenannte bedingte Wahrscheinlichkeiten, die auf den folgenden Seiten erläutert werden.
Regel (5): Multiplikationssatz für unabhängige Ereignisse
 |
|---|