Lektion 3 - Wahrscheinlichkeitsbegriffe und Kombinatorik
In dieser Lektion lernen Sie,
- die Regeln für die Durchführung eines Zufallsexperiments,
- Ergebnisse und Ereignisse kennen,
- die grundlegenden Formeln und Rechenregeln für die Wahrscheinlichkeit,
- die bedingte Wahrscheinlichkeit kennen.
3.2 Wahrscheinlichkeitsbegriffe
Wir kennen drei verschiedene Begriffe für die Darlegung der Wahrscheinlichkeit
- Statistische Wahrscheinlichkeit
- Klassische Wahrscheinlichkeit (nach Laplace)
- Axiomatische Wahrscheinlichkeit (nach Kolmogoroff)
Die statistische Wahrscheinlichkeit
Die statistische Wahrscheinlichkeit P(A) ist derjenige Wert, bei dem sich die relative Häufigkeit h(A) bei einer zunehmenden Zahl von Zufallsexperimenten stabilisiert:
![]()
Die klassische Wahrscheinlichkeit
Die klassische oder mathematische Wahrscheinlichkeit ist der Quotient aus der Anzahl der für das Ereignis A günstigen Fälle und der Anzahl aller möglichen Fälle:
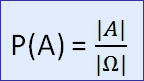
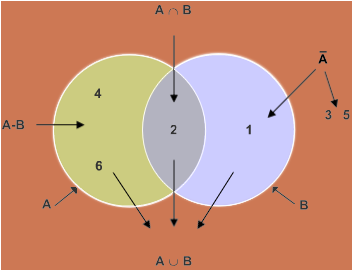
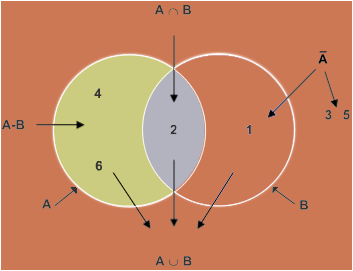
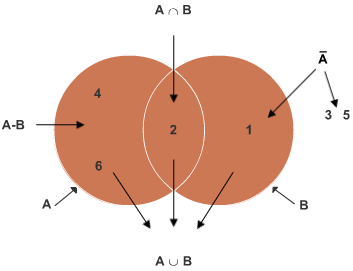
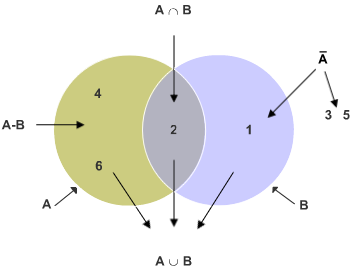
Geben Sie die sechs Wahrscheinlichkeiten für das nachfolgende Venn-Diagramm an:
Das Venn-Diagramm
...Beispiel für Ω = {1,2,3,4,5,6} eines Würfels
 |
Die Grundregeln der Wahrscheinlichkeitsrechnung beziehen sich auf das unmögliche Ereignis, das Komplementärereignis und die Vereinigung beliebiger Ereignisse. Antwort: Mauszeiger auf die Begriffe (Mouseover) |
Die axiomatische Wahrscheinlichkeit
Axiom 1
Jedem Ereignis A ist eine reelle Zahl größer gleich 0 und kleiner gleich 1 zugeordnet, die Wahrscheinlichkeit P(A) heißt:
Axiom 2
Die Wahrscheinlichkeit für das sichere Ereignis ist gleich 1:
Axiom 3
Die Wahrscheinlichkeit für das Vereinigungsereignis zweier disjunkter Ereignisse ist die Summe der beiden Wahrscheinlichkeiten:
Die axiomatische Wahrscheinlichkeit am Würfelbeispiel
zu Axiom 1: P(A) = 0,5 das entspricht 50%
zu Axiom 2: Die Wahrscheinlichkeit, eine 1,2,3,4,5 oder 6 zu werfen, ist 1 bzw. 100%
zu Axiom 3: A und Ā sind disjunkt.
Die Wahrscheinlichkeitssumme ist 1.
Kreuztabelle für verknüpfte Ereignisse
Die Kreuztabelle ist eine wichtige Darstellungsform für die Verknüpfungen von Ereignissen:
| Zufriedenheit | ja | nein | Summe | |
| Geschlecht | B | |||
| männlich | A | 0,54 | 0,06 | 0,60 |
| weiblich | Ā | 0,36 | 0,04 | 0,40 |
| Summe | 0,90 | 0,10 | 1,00 | |
Die Kreuztabelle enthält Randwahrscheinlichkeiten und Wahrscheinlichkeiten für die kombinierten Ausprägungen.
Wir erkennen in der obigen Tabelle, dass - wegen der vorliegenden Unabhängigkeit - die Zellenwahrscheinlichkeiten als Produkte der Randwahrscheinlichkeiten zustande kommen.